Chequeo de supuestos

0. Objetivo

El objetivo de este práctico es aprender cómo analizar el cumplimiento de supuestos de regresión lineal con performance.

1. Paquetes y datos a utilizar

En este caso utilizaremos diversos paquetes, entre los cuales el más relevante será performance, que se utilizará para evaluar la calidad de los modelos estimados. Utilizaremos los datos sobre precios medianos de casas del paquete wooldridge.

pacman::p_load(wooldridge, #Para descargar los datos
               summarytools, #decriptivos
               sjPlot, #visualización
               performance, #evaluación de modelos
               lmtest, #Para el test RESET de Ramsey
               see) # herramientas para la visualización
options(scipen=999)
data("hprice2")

2. El ajuste y la calidad de los modelos de regresión lineal

En prácticos anteriores hemos revisado diversas maneras de abordar el ajuste y la calidad de los modelos que estimamos. En el fondo, estadístico como \(R^2\), \(F\), \(p-valores\), entre otros, entregan información acerca de qué tan bien explica nuestro modelo la variabilidad de \(y\).

No obstante, como hemos revisado a lo largo del curso, para poder asegurar la calidad y robustez de los modelos de regresión lineal que estimamos, debemos demostrar que esto cumplimen con algunos supuestos fundamentales. En este práctico utilizaremos el paquete performance y sus diversas funciones para aprender cómo chequear, comprender y analizar estos supuestos.

A lo largo de este práctico analizaremos el siguiente modelo

mod = lm(lprice ~ crime + rooms + stratio + lowstat ,data = hprice2)
summary(mod)

## 
## Call:
## lm(formula = lprice ~ crime + rooms + stratio + lowstat, data = hprice2)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.68869 -0.11254 -0.02062  0.10091  0.92711 
## 
## Coefficients:
##              Estimate Std. Error t value             Pr(>|t|)    
## (Intercept) 10.152054   0.161954  62.685 < 0.0000000000000002 ***
## crime       -0.009718   0.001253  -7.754    0.000000000000050 ***
## rooms        0.127981   0.017370   7.368    0.000000000000719 ***
## stratio     -0.033592   0.004840  -6.940    0.000000000012148 ***
## lowstat     -0.028348   0.001818 -15.589 < 0.0000000000000002 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2127 on 501 degrees of freedom
## Multiple R-squared:  0.7319, Adjusted R-squared:  0.7298 
## F-statistic:   342 on 4 and 501 DF,  p-value: < 0.00000000000000022

Podemos ver que todos los coeficientes estimados son estadísticamente significativos. Asimismo, salvo \(rooms\), el efecto de todo el resto de variables explicativas sobre los precios medianos de las casas de los barrios analizados es negativo. El estadístico \(R^2\) se aproxima a \(0.73\), y el estadístico \(F\) es estadísticamente significativo. De tal modo, es posible demostrar evidencia respecto de la validez estadística de nuestro modelo, así como de su bondad de ajuste. Revisemos ahora el cumplimiento de supuestos del modelo de regresión lineal propuestos por Gauss-Markov (Wooldridge, 2015).

3. Linealidad

El primer supuesto es que la regresión especificada es lineal en sus parámetros. Ello quiere decir que se espera que exista una relación lineal entre las variables explicada e explicativas.

Podemos saber si se cumple este supuesto a partir de un gráfico de dispersión de datos, que relacione ambas variables, y verificar de manera “intuitiva” si la tendencia de esta relación se puede describir por una línea recta. El paquete performace nos permite hacer esto con su función check_model indicando en el argumento check = "ncv

check_model(mod, check = c("ncv", "linearity"))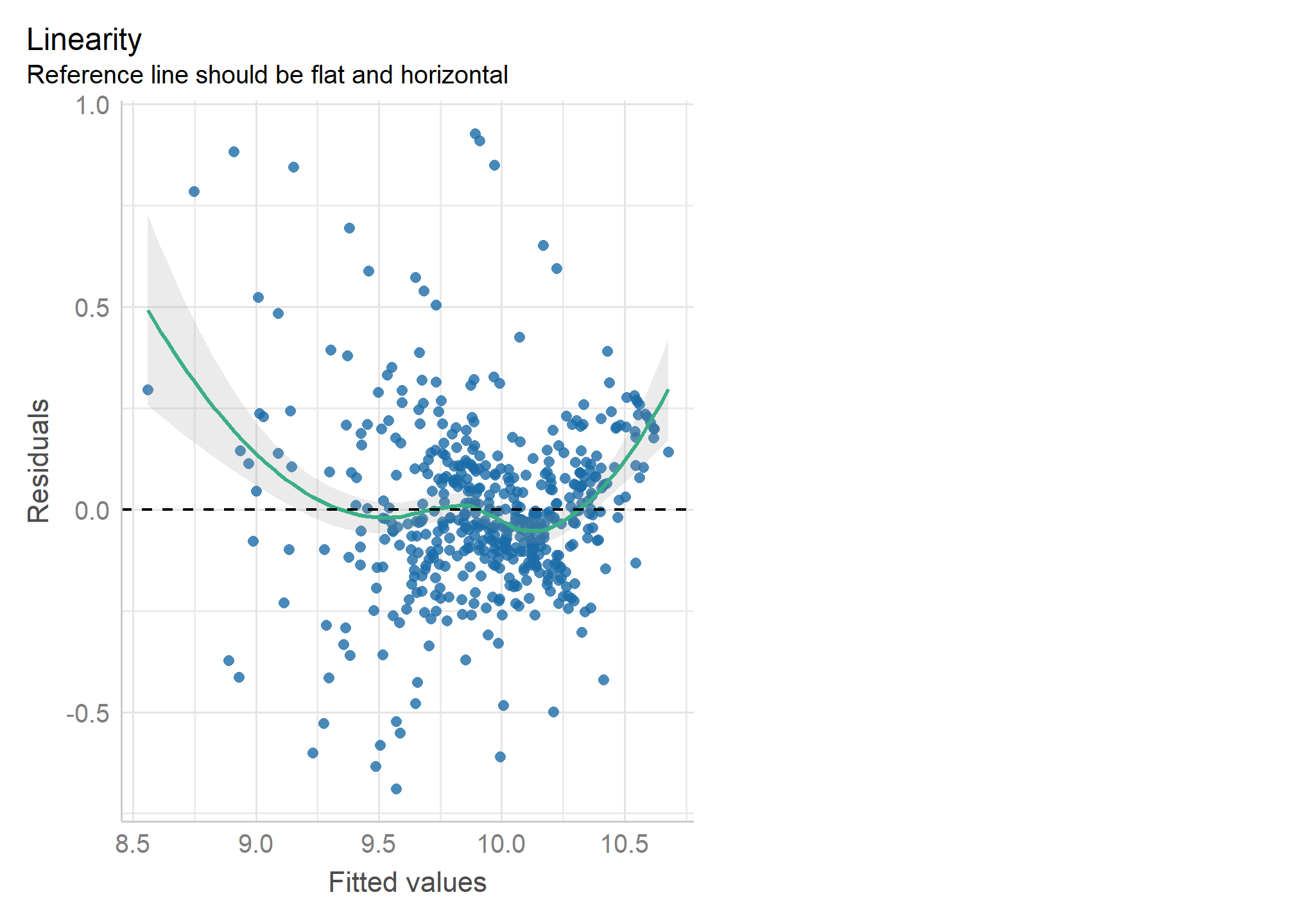

Este gráfico presenta la relación entre los valores predichos para \(y\) y los residuos estimados. La línea punteada indica cómo debiesen dispersarse los puntos azules (que corresponden a la intersección de los valores predichos y los residuos estimados para cada individuo) en caso de que existiese linealidad. En este caso es posible apreciar que la relación no se aproxima a la linealidad.

En caso de que el cumplimiento no sea claro, una forma numérica para chequear este supuesto es que el valor promedio de los residuos sea cero. En este caso, ese valor es igual a 0. Si esto no fuera así, los residuos estarían sesgados sistemáticamente, por lo cual el supuesto de linealidad no se cumpliría. De suceder aquello, el modelo debiese re-especificarse (medir de otra manera la variable) en algún término de la ecuación de regresión al cuadrado o al cubo. Un modo que se ocupa para testear la necesidad de esta re-especificación es el test RESET de Ramsey que indica que:

\(H_0\) cuando el modelo tiene algún término al cuadrado o cubo, la media de los residuos es cero. Es decir: si no podemos rechazar \(H_0\), nuestro modelo está bien especificado (es decir, es lineal).

Utilizaremos resettest de lmtest para comprobar el cumplimiento del test RESET, estimando un \(p\)-valor con el cual podremos rechazar la hipótesis nula

lmtest::resettest(mod)

## 
##  RESET test
## 
## data:  mod
## RESET = 28.484, df1 = 2, df2 = 499, p-value = 0.000000000001933

Aquí podemos ver que no podemos rechazar \(H_0\), por lo cual debiésemos re-especificar el modelo.

4. Homocedasticidad

Homoce ¿qué? Sí, homocedasticidad. Este concepto indica que los residuos se distribuyen de forma homogénea (por eso el sufijo homo). Como ya podrás haber notado este supuesto se vincula con el de linealidad. Y, al igual que este, también puede comprobarse con un gráfico de dispersión entre la variable explicada (\(y\)) e explicativa (\(x\)), donde podamos ver de manera clara la recta de regresión estimada y la distribución de los residuos. Aceptaremos el supuesto de homocedasticidad si la variación de los residuos es homogénea: es decir, no veremos un patrón claro, sino más bien se distribuirán de forma aleatoria. De manera gráfica veremos una nube de puntos que tiene una forma similar en todo el rango de las observaciones de la variable explicativa.

Para comprobar el supuesto de homocedasticidad de manera más certera utilizaremos la prueba Breusch-Pagan Godfrey cuya hipótesis nula indica que

\(H_0\): La varianza de los residuos del modelo de regresión no es constante (heterocedasticidad)

En este caso, buscaremos que rechazar la \(H_0\). Esto implicaría que, “en suma y resta”, si bien hay residuos, estos tienen una variación homogénea en todos los tramos de la relación de la variable explicada con la explicativa.

A partir de la función check_heteroscedasticity verificaremos qué ocurre con la hipótesis nula

check_heteroscedasticity(mod)

## Warning: Heteroscedasticity (non-constant error variance) detected (p < .001).

En este caso, el test nos indica que la varianza no es homocedástica, por lo cual aceptamos la hipótesis nula de que la varianza de los residuos no es constante.

5. Normalidad de residuos

Además de la linealidad (media 0), la homocedasticidad (varianza mínima y constante), el método de estimación de la regresión lineal (OLS o MCO en español) requiere asegurar una distribución normal de los residuos pues, en caso contrario, el modelo no es consistente a través de las variables y observaciones. Esto significa que los errores no son aleteatorios, sino sistemáticos.

Al igual que con los otros supuestos, la normalidad de los residuos se puede evaluar con métodos numéricos, utilizando pruebas que ya conocemos de otros cursos como la prueba de Shapiro-Wilk y Kolmogorov-Smirnov

A partir de la función check_normality utilizaremos la prueba Shapiro-Wilk para ver qué ocurre con la hipótesis nula a

check_normality(mod)

## Warning: Non-normality of residuals detected (p < .001).

En este caso, no podemos rechazar la hipótesis nula de que los residuos no se distribuyen normalmente, por lo cual no podemos afirmar que los errores en nuestras estimación son aleatorios.

6. Independencia

Evidentemente si los residuos no siguen una distribución normal, es probable que estos no sean independientes entre sí. Esto significa que buscaremos que los errores asociados a nuestro modelo de regresión sean independientes. Para saber si se cumple ese criterio se utiliza la prueba de Durbin-Watson, donde la \(H_0\) supone que los residuos son independientes.

A partir de la función check_autocorrelation utilizaremos la prueba Durbin-Watson para ver qué ocurre con la hipótesis nula a

check_autocorrelation(mod)

## Warning: Autocorrelated residuals detected (p < .001).

El \(p-valor\) estimado nos indica que no podemos rechazar la hipótesis nula de que los residuos son independientes.

En síntesis, sabemos la regresión lineal requiere de una relación lineal entre sus variables explicativas y explicada. Para ello no solo es importante chequear la distribución de los residuos, sino dos posibilidades que pueden tendenciar esa relación lineal: como casos influyentes en la muestra y predictores que están altamente relacionados. Revisaremos la última de estas

7. Multicolinealidad

La multicolinealidad es la relación de dependencia lineal fuerte entre más de dos predictores de un modelo.

El problema que produce es que será difícil cuantificar con exactitud el efecto de cada predictor sobre la variable explicada, precisamente pues puede ocurrir que el efecto que una variable predictora tenga sobre el fenómeno que se busca estudiar dependa del valor de otra variable del modelo.

Para la regresión múltiple esto implica un problema, pues suponemos que podemos “controlar” por el otro valor de la variable. Si los predictores están correlacionados fuertemente, entonces el efecto de una variable \(x_1\) sobre \(y\) estará “contaminado” por el efecto de otra variable \(x_2\) sobre \(y\), y vice-versa.

Podemos examinar esta relación endógena entre predictores a partir de la existencia de altas correlaciones (lineales) entre variables. La aproximación numérica más utilizada es el VIF (factor de inflación de varianza), que indica hasta qué punto la varianza de los coeficientes de regresión se debe a la colinealidad (o dependencia) entre otras variables del modelo.

Para evaluar esto ocuparemos el comando check_collinearity(). Como podemos ver en el gráfico, todos los valores son menores a 5 (como recomienda el paquete).

plot(check_collinearity(mod))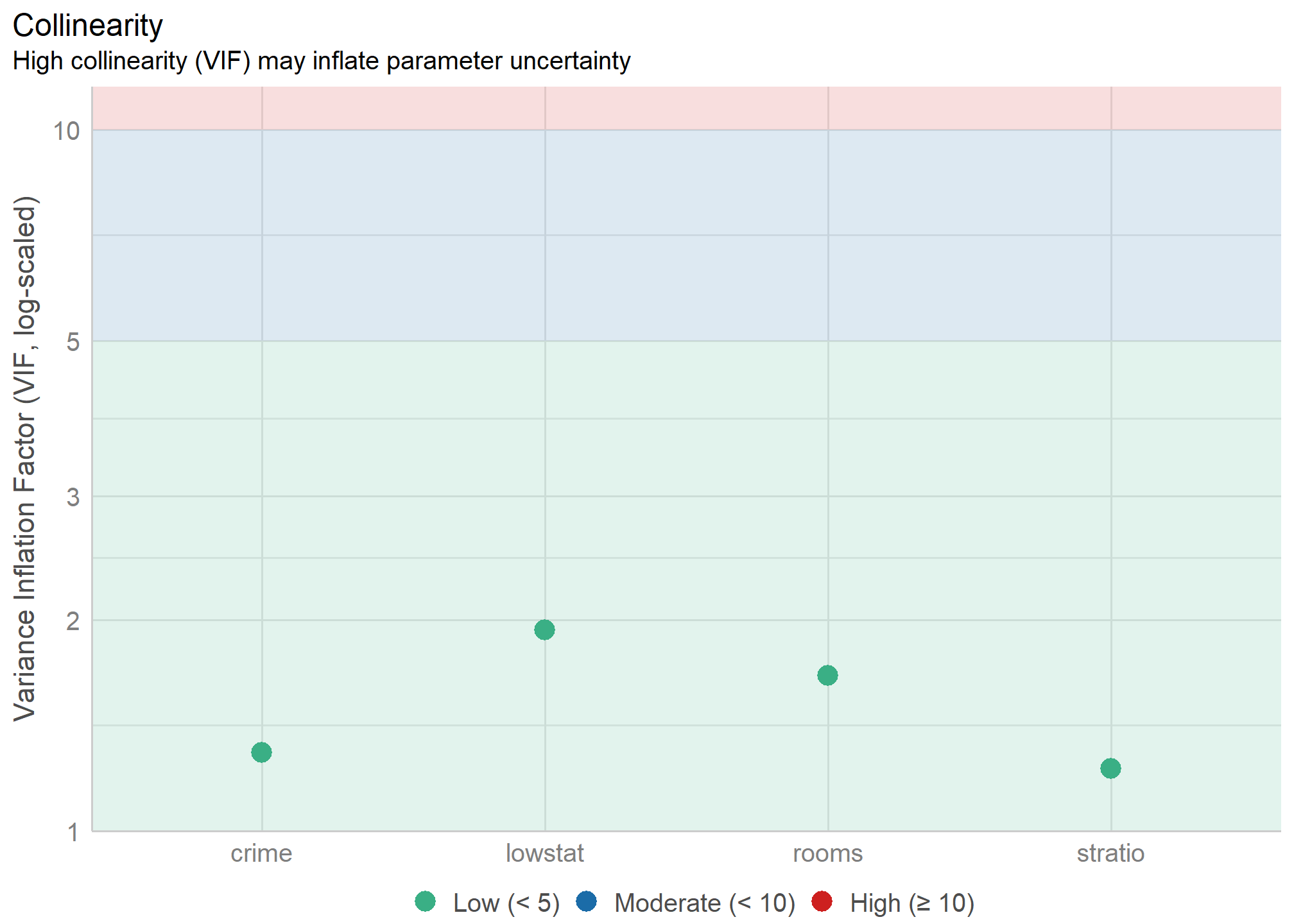

Ahora bien, dado que sabemos que las correlaciones en ciencias sociales nunca son tan altas, un criterio que se ocupa en nuestras disciplinas para evaluar multicolinealidad es es evitar valores del VIF mayores a 2.5.

check_collinearity(mod)

## # Check for Multicollinearity
## 
## Low Correlation
## 
##     Term  VIF Increased SE Tolerance
##    crime 1.29         1.14      0.77
##    rooms 1.66         1.29      0.60
##  stratio 1.23         1.11      0.82
##  lowstat 1.93         1.39      0.52

Los valores especificados en la columna VIF indican que no existe una fuerte correlación entre las variables explicativas. Para solucionar este problema, se podría eliminar alguno de los predictores problemáticos, o evaluar si es que estas variables más bien son parte de un mismo constructo.

8. Casos influyentes

Un último supuesto que revisaremos, y es el que probablemente el que más nos enfrentamos en las ciencias sociales, son los casos influyentes (también llamados outliers en inglés). Un ejemplo claro de esto son las variables como ingresos, donde muchas veces tenemos casos extremos con muy bajos salarios y otros muy altos, y que pueden tendenciar nuestras rectas de regresión pese a que no es evidente una relación lineal(o algún tipo de relación) entre la variable explicativa y explicada.

Para verificar si un caso es influyente, examinaremos si la ausencia o presencia de ese caso genera un cambio importante en la estimación del modelo de regresión. Este enfoque se aborda a partir del cálculo de la Distancia de Cook (Cook,1977)

Primero podemos graficar la influencia de los casos con check_outliers() dentro de un plot()

plot(check_outliers(mod))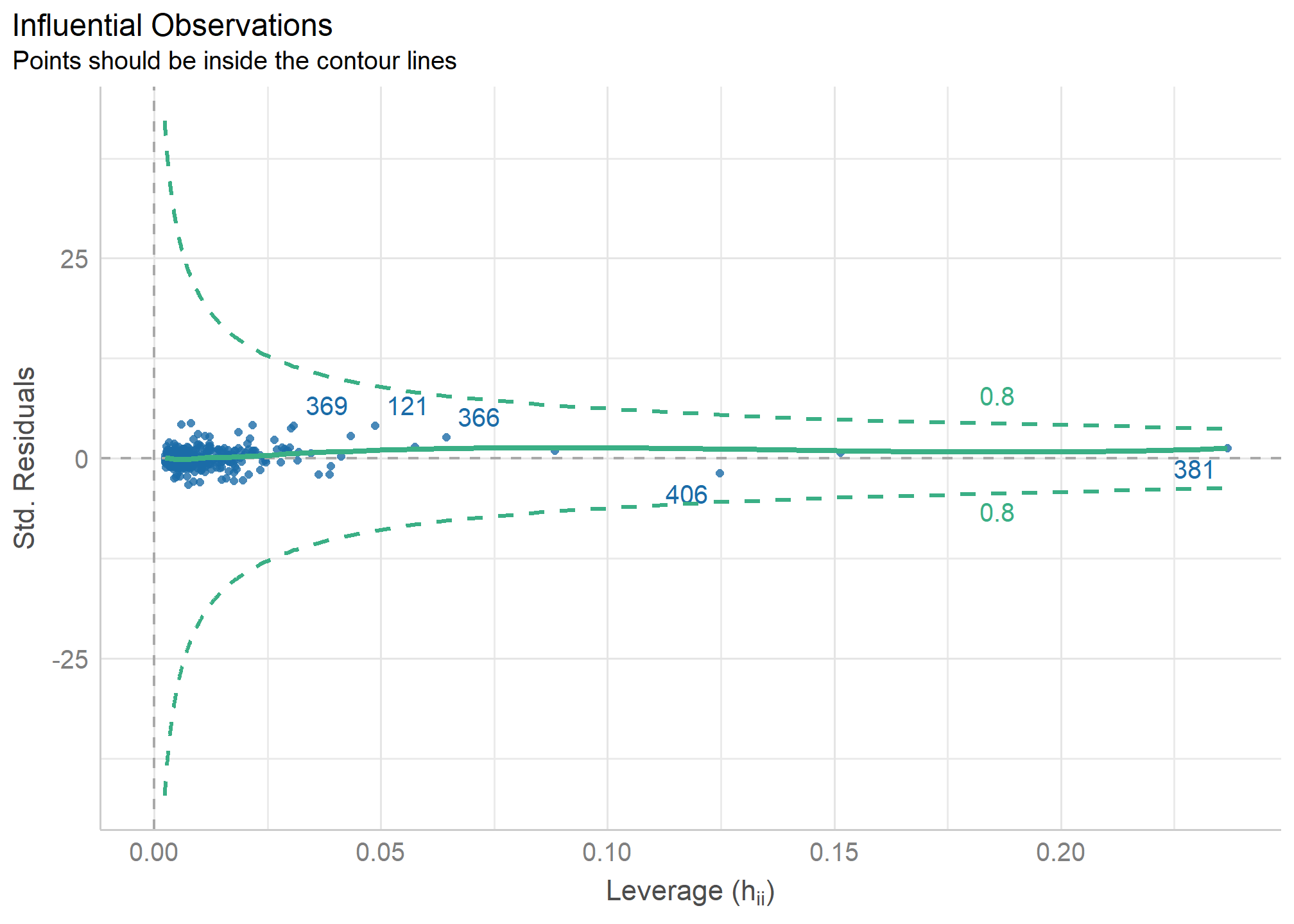

Luego para verificar si la ausencia o presencia de eliminar algunos de estos casos que presentan mayor distancia producen una diferencia significativa en la estimación del modelo, realizamos

check_outliers(mod)

## OK: No outliers detected.

✔️ No se detectaron casos atípicos.

Resumen

En este práctico aprendimos a analizar los supuestos del teorma de Gauss-Markov a través del paquete performance.