Regresión lineal múltiple y predictores categóricos

0. Objetivo del práctico

El presente práctico tiene dos objetivos:

Aprender a estimar una regresión lineal múltiple en R con lm().
Aprender a interpretar modelos de regresión lineal múltiple con variables explicativas categóricas.

Materiales de la sesión

Tal como en la sesión anterior, en este práctico se utilizarán los datos sobre salarios utilizados en el capítulo 2 del libro Introducción a la econometría de J.W. Wooldridge (2015). En este caso, cargaremos los datos ya procesados.

data = readRDS(url("https://github.com/statistics-R/practico-7/raw/main/data.rds"))

Asimismo, la realización de este práctico requiere la carga de diversos paquetes que nos permitirán explorar los datos y presentar los modelos estimados.

if (!require("pacman")) install.packages("pacman") # Instalamos pacman en caso de necesitarlo
pacman::p_load(wooldridge, #Para descargar los datos
               dplyr, #Para procesar datos
               ggplot2,#Para graficar
               sjmisc, #Para explorar los datos
               sjPlot, #Para explorar los datos
               texreg) #Para presentar el modelo de regresión estimado

1. Volviendo a explorar los datos

Volvemos a encontrarnos con:

wage ( $y$ ): indica el salario por hora en miles de pesos de cada persona en los datos.
educ ( $x_{1}$ ): indica el número de años de escolaridad de cada persona en los datos.
exper ( $x_{2}$ ): indica los años de experiencia laboral de cada persona en los datos.

Sin embargo, ahora agregamos una variable categórica:

rama ( $x_{3}$ ) : actividad económica a la que se dedica la empresa donde trabaja.

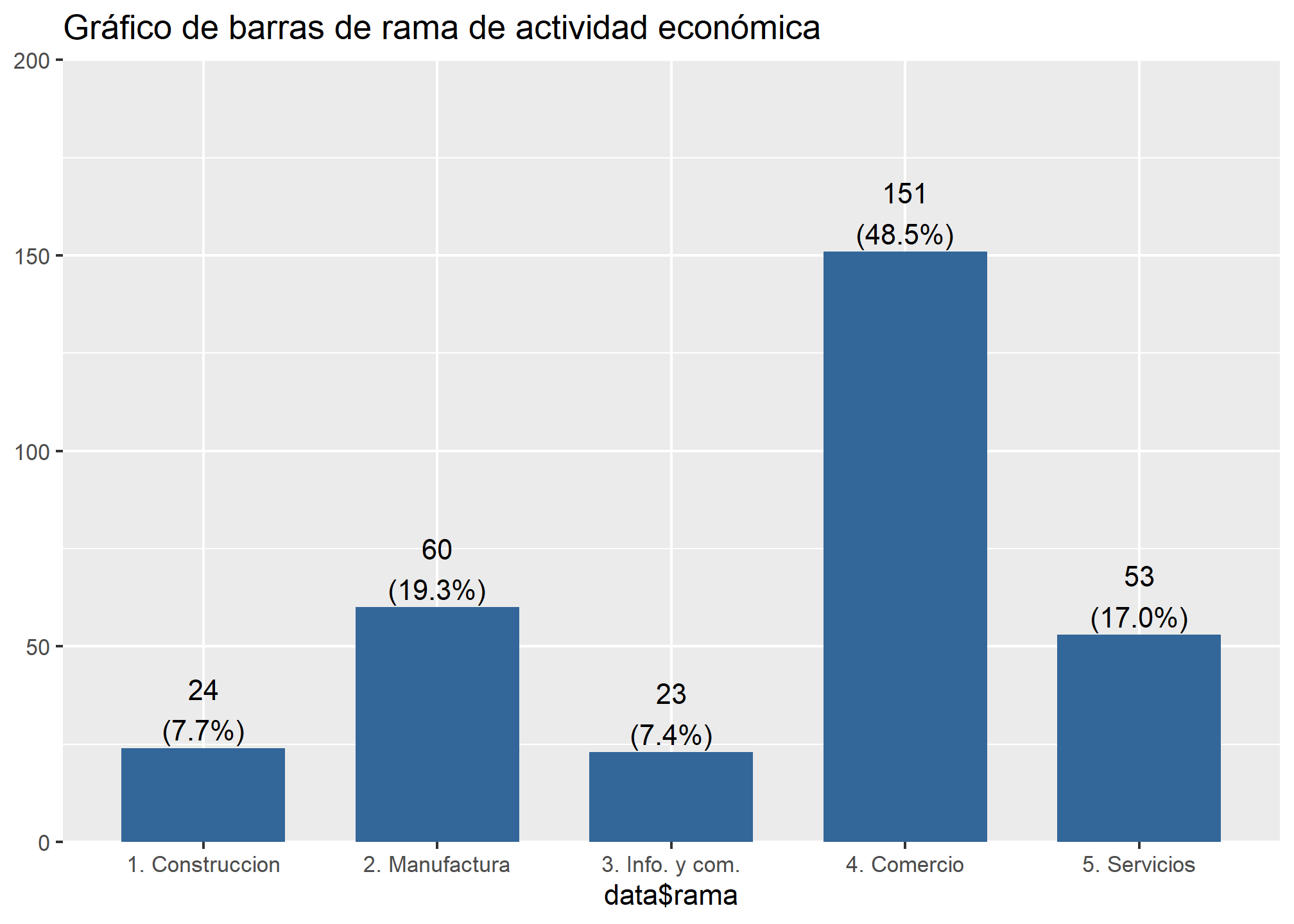
Utilicemos frq() de sjmisc para explorar esta nueva variable. Podemos ver que casi el 50% de la muestra trabaja en comercio.

Las seleccionaremos utilizando la función select() de dplyr, a modo de trabajar con un set de datos más acotado

Recordemos la distribución de estas variables:

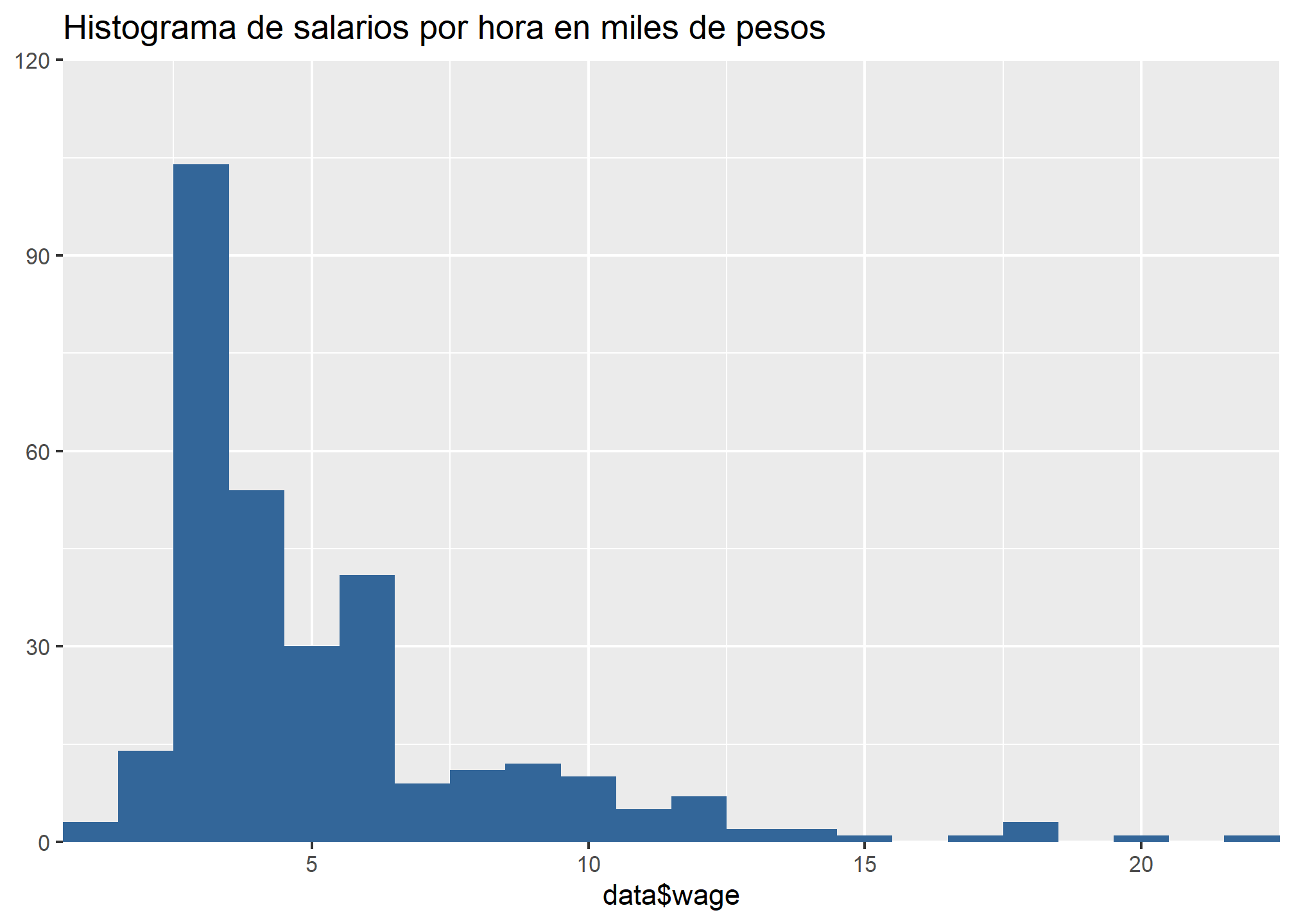
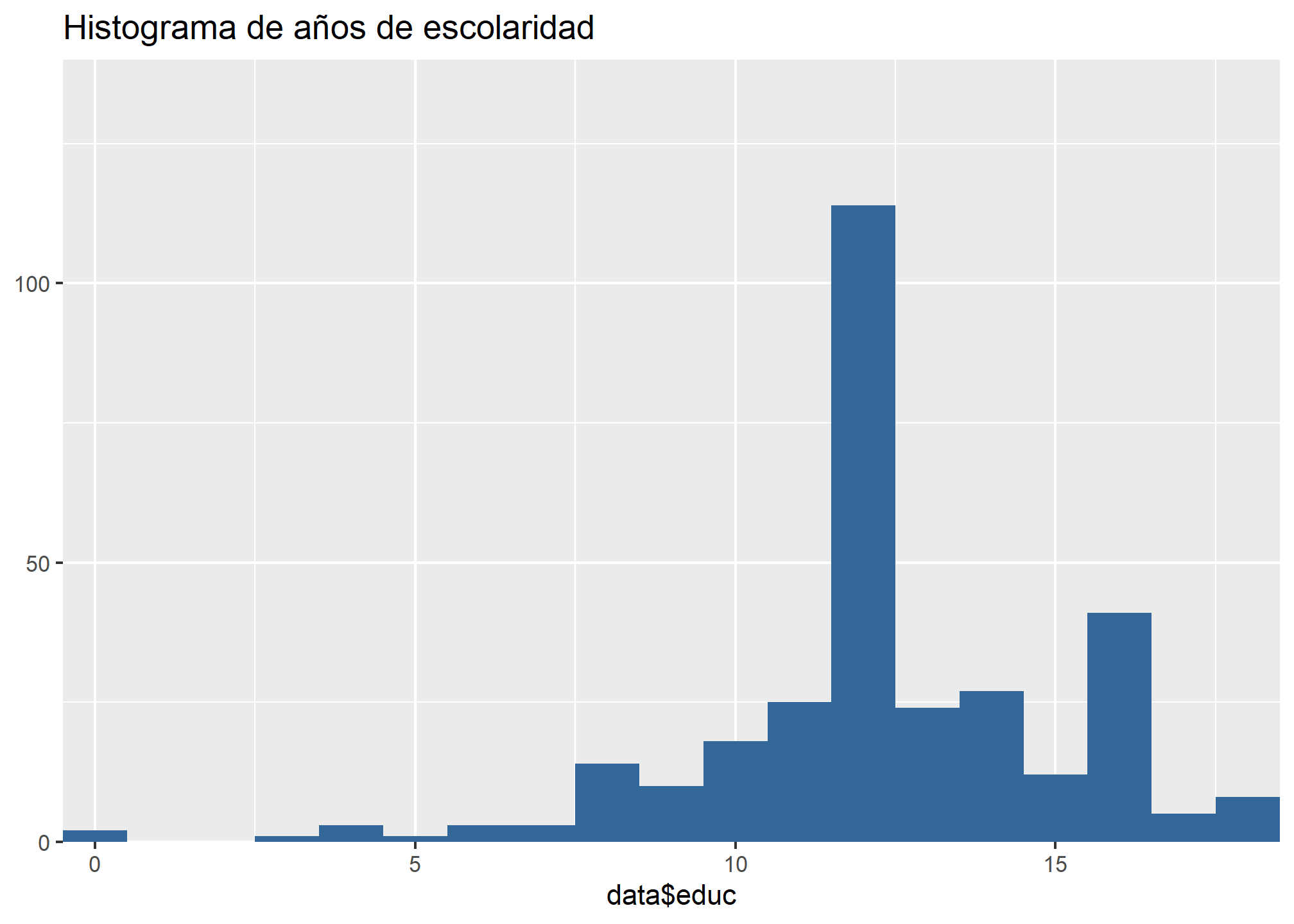
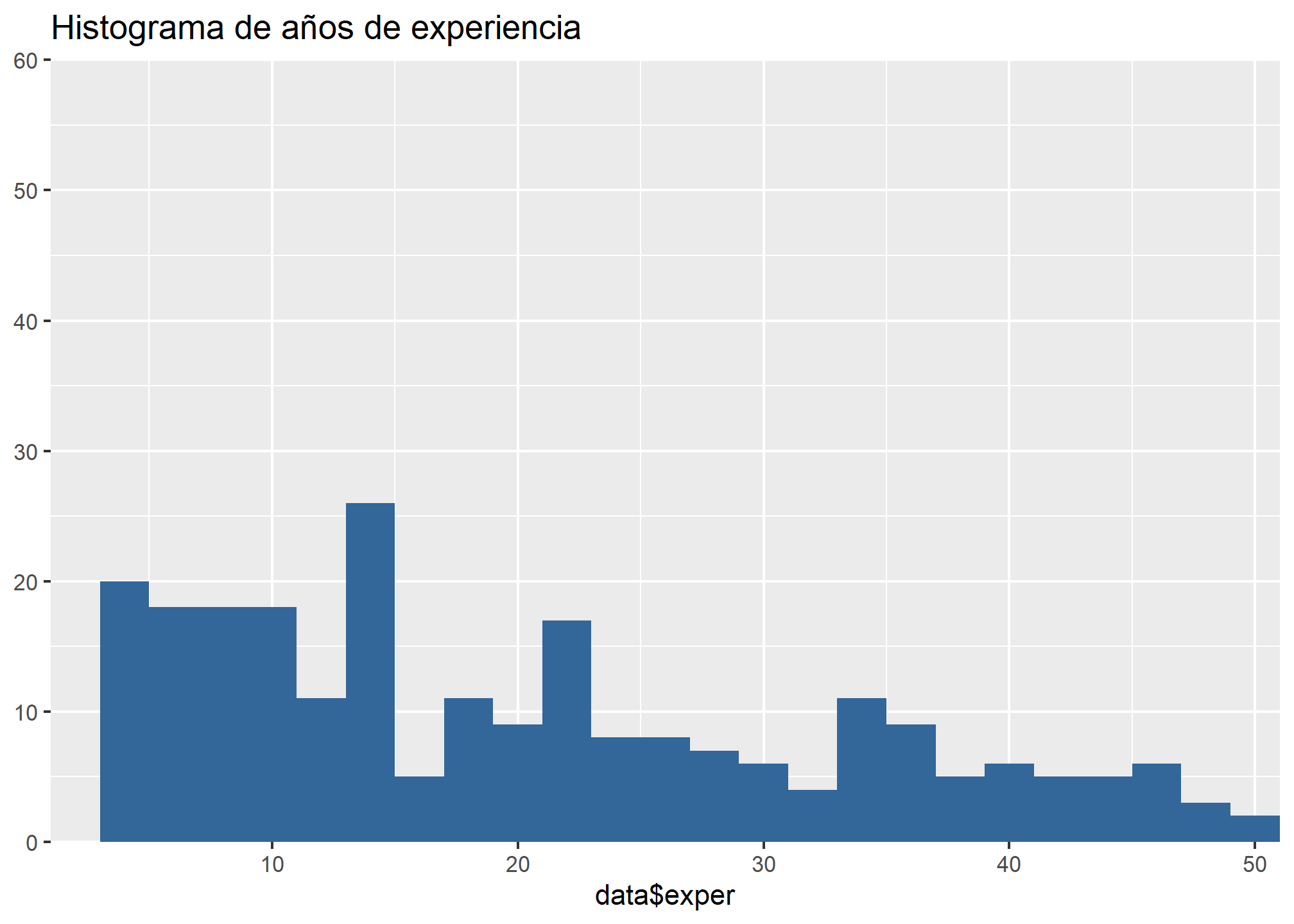
Podríamos preguntarnos cómo se distribuyen los salarios por hora en cada actividad económica

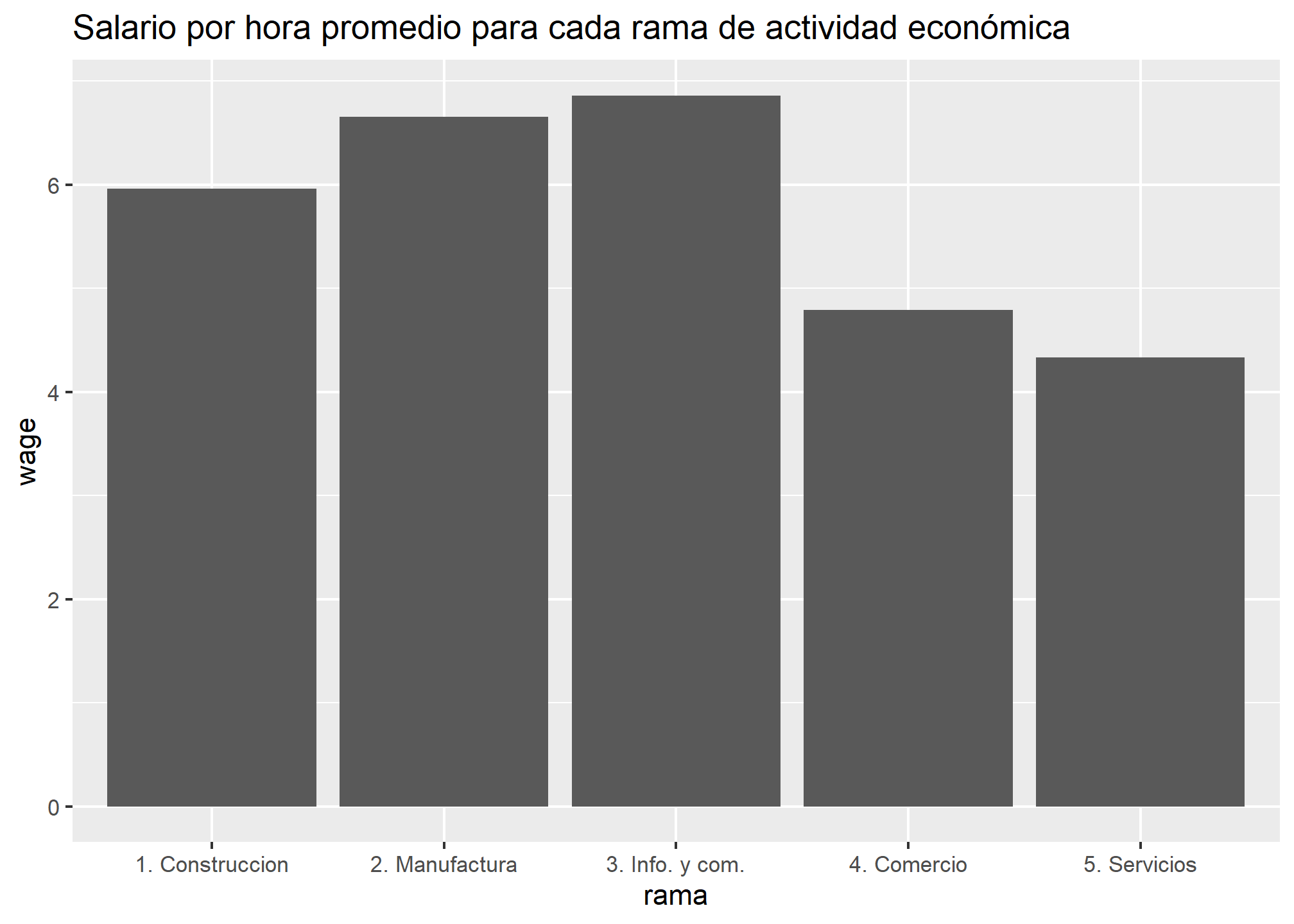Vemos que Información y comunicaciones presenta el promedio más alto (6.86 mil), seguido por Manufactura (6.65 mil) y Construcción (5.96 mil). Por su parte, los promedios más bajos corresponden a Servicios (4.34 mil) y Comercio (4.79 mil).

En este caso, la variable por explicar sigue siendo wage ( $y$ ), a partir de la cual estimaremos un modelo de regresión lineal múltiple sobre educ ( $x_{1}$ ), exper ( $x_{2}$ ) y rama ( $x_{3}$ ). Sin embargo, la inclusión de un predictor categórico requiere de una categoría de referencia con base en la cual sea posible estimar diferencias promedio para cada una de las otras categorías. En el modelo por estimar, esto se reflejará en la estimación de $k - 1$ coeficientes de regresión, siendo $k$ el número de categorías que presenta nuestra variable explicativa categórica. En este caso, $k_{r a m a} = 5$ , de modo que el modelo estimado presentará 4 coeficientes de regresión para la actividad económica, donde cada uno de ellos reflejará las diferencias promedio estimadas respecto de la categoría de referencia.

Pero ¿qué es una categoría de referencia? Por defecto, en nuestras variables categóricas corresponde al primer valor de la variable, siguiendo una prioridad alfanumérica. Ello quiere decir que las categorías que inicien con el número “1” tiene más prioridad que las que inician con el número “4”, así como que las categorías que inician con la letra “a” tienen una mayor prioridad frente a las que inician con “d”. Podemos utilizar la función factor() para modificar manualmente el orden de nuestras variables categóricas (cuyo tipo de dato debe ser factor). A modo de ejemplo, crearemos

Una nueva variable que tenga como categoría de referencia el valor 3. Info. y com., utilizando la función ref_lvl() de sjmisc, y
Una nueva variable factor cuyos niveles sigan el promedio de salarios por hora para cada categoría de actividad económica:

#Transformamos nuestra variable en factor
data$rama = factor(data$rama)
#Creamos una nueva variable con 3. Info y com. como categoría de referencia
data$rama_info = ref_lvl(data$rama, lvl = "3. Info. y com.")
#Y otra con la que ordenamos las categorías de forma ascendente a partir de los promedios en wage
data$rama_wage = factor(data$rama, levels = c("5. Servicios",
                                              "4. Comercio", 
                                              "1. Construccion", 
                                              "2. Manufactura",
                                              "3. Info. y com."))

Un modelo de regresión lineal múltiple con predictores categóricos se puede expresar a partir de la siguiente ecuación:

$\hat{y} = β_{0} + β_{1} x_{i 1} + β_{2} x_{i 2} + β_{3} x_{k = k + 1}, . . ., β_{3} x_{k = k}$ Donde

$β_{0}$ : Corresponde al intercepto de regresión.
$β_{1}$ : Corresponde a la pendiente estimada para la función de regresión lineal de los salarios por hora ( $y$ ) sobre los años de escolaridad ( $x_{1}$ ). Así, por cada unidad que aumente $x_{1}$ (en este caso, por cada año de escolaridad extra), el valor estimado $\hat{y}$ para los salarios por hora aumentará o disminuirá en $β_{1}$ .
$β_{2}$ : Corresponde a la pendiente estimada para la función de regresión lineal de los salarios por hora ( $y$ ) sobre los años de experiencia laboral ( $x_{2}$ ). Así, por cada unidad que aumente $x_{1}$ (en este caso, por cada año de experiencia laboral), el valor estimado $\hat{y}$ para los salarios por hora aumentará o disminuirá en $β_{2}$ .
$β_{3} x_{k = k + 1}$ , …, $β_{3} x_{k = k}$ : Corresponde al coeficiente de regresión estimado para cada una de las categorías de nuestra variable explicativa categórica. En este caso tenemos 5 categorías, de modo que estimaremos 4 coeficientes, que en este caso reflejarán las diferencias promedio de los salarios estimados para quienes se desempeñan en construcción, manufactura, información y comunicaciones, comercio y servicios. Estos, sumados al intercepto $β_{0}$ , indican las diferencias promedio estimadas para cada una de las categorías de actividad económica.

En este caso, lo esperable es que los valores predichos para información y comunicaciones sean mayores que aquellos estimados para el resto de categorías ocupacionales, siguiendo lo presentado en el gráfico de barras anteriormente presentado.

2. Estimando modelos de regresión lineal múltiple con predictores categóricos con `lm()`

Como vimos en el práctico anterior, para agregar una nueva variable explicativa a nuestros modelos sólo basta con agregar + variable en nuestro primer argumento. Estimaremos también los modelos con distintas categorías de referencia para compararlos:

$\hat{w a g e} = β_{0} + β_{1} e d u c_{i} + β_{2} e x p e r_{i} + β_{3} r a m a_{2. M a n u f a c t u r a} + β_{3} r a m a_{3. I n f o . y c o m .} + β_{3} r a m a_{4. C o m e r c i o} + β_{3} r a m a_{5. S e r v i c i o s}$

m1 = lm(wage ~ educ + exper +rama, data = data)
m2 = lm(wage ~ educ + exper +rama_info, data = data)
m3 = lm(wage ~ educ + exper + rama_wage, data = data)
#Estimamos también los modelos anteriores para comparar ajustes
m4 = lm(wage ~ educ, data = data)
m5 = lm(wage ~ exper, data = data)
m6 = lm(wage ~ educ + exper, data = data)

## 
## ================================================================================================
##                           Modelo 1    Modelo 2    Modelo 3    Modelo 4    Modelo 5    Modelo 6  
## ------------------------------------------------------------------------------------------------
## (Intercept)                -0.31       -0.63       -2.45 **     0.13        4.91 ***   -1.83 *  
##                            (0.97)      (1.11)      (0.93)      (0.77)      (0.29)      (0.87)   
## educ                        0.48 ***    0.48 ***    0.48 ***    0.42 ***                0.50 ***
##                            (0.06)      (0.06)      (0.06)      (0.06)                  (0.06)   
## exper                       0.05 ***    0.05 ***    0.05 ***                0.02        0.06 ***
##                            (0.01)      (0.01)      (0.01)                  (0.01)      (0.01)   
## rama2. Manufactura         -0.18                                                                
##                            (0.70)                                                               
## rama3. Info. y com.        -0.33                                                                
##                            (0.85)                                                               
## rama4. Comercio            -1.64 **                                                             
##                            (0.63)                                                               
## rama5. Servicios           -2.14 **                                                             
##                            (0.71)                                                               
## rama_info1. Construccion                0.33                                                    
##                                        (0.85)                                                   
## rama_info2. Manufactura                 0.14                                                    
##                                        (0.71)                                                   
## rama_info4. Comercio                   -1.31 *                                                  
##                                        (0.65)                                                   
## rama_info5. Servicios                  -1.82 *                                                  
##                                        (0.72)                                                   
## rama_wage4. Comercio                                0.50                                        
##                                                    (0.46)                                       
## rama_wage1. Construccion                            2.14 **                                     
##                                                    (0.71)                                       
## rama_wage2. Manufactura                             1.96 ***                                    
##                                                    (0.54)                                       
## rama_wage3. Info. y com.                            1.82 *                                      
##                                                    (0.72)                                       
## ------------------------------------------------------------------------------------------------
## R^2                         0.24        0.24        0.24        0.13        0.01        0.18    
## Adj. R^2                    0.23        0.23        0.23        0.13        0.01        0.18    
## Num. obs.                 311         311         311         311         311         311       
## ================================================================================================
## *** p < 0.001; ** p < 0.01; * p < 0.05

Lo primero que hay que observar es que, en los tres modelos, $β_{1}$ y $β_{2}$ son iguales. Lo mismo sucede con las medidas de ajuste. Los únicos elementos que se modifican son el intercepto $β_{0}$ y los coeficientes estimados para cada rama de actividad económica. Ello quiere decir que los modelos son esencialmente los mismos, aunque presentan la información de manera diferente. Entonces, ¿cómo ordenar nuestros factores? ello siempre dependerá de nuestros antecedentes teóricos y empíricos. Por ejemplo, nuestra categoría de referencia puede ser aquella de la cual se esperen los valores más bajos o más altos. Asimismo, nuestra categoría de referencia puede ser aquella en la cual queramos centrar nuestro análisis. Por ejemplo, si alguien nos solicitara un análisis para los asalariados del sector servicios, sería recomendable que aquella fuese nuestra categoría de referencia.

Asimismo, podemos ver que la inclusión de este predictor categórico permite aumentar el porcentaje de la varianza explicada de $y$ con el modelo en 5 puntos. El $R^{2}$ de los modelos 1, 2 y 3 es mayor al de los modelos 4, 5 y 6. En este caso, a priori podríamos considerar el que la inclusión de la rama de actividad económica en la explicación de los salarios por hora que reciben las personas de la muestra permite analizar su variabilidad de manera más precisa.

3. Predicción

Utilicemos el modelo 1 para nuestros análisis

$\hat{w a g e} = - 0.3 + .48 e d u c_{i} + .05 e x p e r_{i} + - 0.18 r a m a_{2. M a n u f a c t u r a} + - 0.32 r a m a_{3. I n f o . y c o m .} + - 1.64 r a m a_{4. C o m e r c i o} + - 2.14 r a m a_{5. S e r v i c i o s}$

En base a esa información, podemos señalar que

Manteniendo constantes los años de escolaridad y de experiencia laboral se espera que, en promedio, los valores predichos para quienes trabajan en construcción sean los más altos en la muestra. Esto, pues todos los coeficientes de regresión son negativos.
Así, en promedio, una persona que trabaje en manufactura gane .18 mil pesos por hora menos que alguien que se emplea en construcción, manteniendo constante el resto de factores.
Del mismo modo, es espera que una persona que trabaja en servicios reciba una remuneración -2.14 mil pesos inferior a alguien que labora en el sector de construcción.

Como pueden ver, la manera en que ha quedado especificado el modelo permite analizar inmediatamente las diferencias promedio entre la categoría de referencia (en este caso, construcción) respecto de las $k - 1$ categorías restantes para las cuales se estimó un coeficiente de regresión. Para comparar el resto de categorías entre sí, podemos a) especificar el modelo con otra categoría de referencia; o b) estimar los valores predichos para cada categoría y comparar ceteris paribus. En este caso, los valores predichos son:

Construcción = $- 0.31$
Manufactura = $- 0.31 - 0.18 = - 0.49$
Información y comunicaciones = $- 0.31 - 0.18 = - 0.63$
Comercio = $- 0.31 - 1.64 = - 1.95$
Servicios = $- 0.31 - 2.14 = - 2.45$

Como podemos ver, los valores esperados indicarían que quienes trabajan en servicios debiese tender a presentar, en promedio, salarios por hora inferiores al resto de actividades económicas. Asimismo, se espera que quienes se desempeñan obtengan, en promedio, salarios $- 0.63 - - 1.95 = 1.32$ mil pesos inferiores que quienes se dedican a la información y las comunicaciones; y así.

Resumen

En este práctico aprendimos a analizar predictores categóricos en modelos de regresión lineal múltiple.

Last updated on April 19, 2023