Regresión lineal múltiple
0. Objetivo del práctico
El presente práctico tiene dos objetivos:
Comprender las implicancias de la incorporación de más de un predictor en modelos de regresión lineal.
Aprender a estimar una regresión lineal múltiple en R con
lm().
Materiales de la sesión
Tal como en la sesión anterior, en este práctico se utilizarán los datos sobre salarios utilizados en el capítulo 2 del libro Introducción a la econometría de J.W. Wooldridge (2015).
Asimismo, la realización de este práctico requiere la carga de diversos paquetes que nos permitirán explorar los datos y presentar los modelos estimados.
if (!require("pacman")) install.packages("pacman") # Instalamos pacman en caso de necesitarlo
pacman::p_load(wooldridge, #Para descargar los datos
dplyr, #Para procesar datos
sjmisc, #Para explorar los datos
sjPlot, #Para explorar los datos
srvyr, #Para crear un objeto encuesta
survey, #Para realizar estimaciones incorporando el diseño muestral
texreg) #Para presentar el modelo de regresión estimado
data("wage1") #Cargamos los datos
wage1 = select(wage1, wage, educ, exper) #Seleccionamos sólo las variables por analizar1. Volviendo a explorar los datos
Si bien en este práctico volveremos a analizar el efecto de los años de escolaridad sobre los salarios por hora, ahora incorporaremos una nueva variable explicativa: los años de experiencia laboral.
- wage (\(y\)): indica el salario por hora en miles de pesos de cada persona en los datos.
- educ (\(x_1\)): indica el número de años de escolaridad de cada persona en los datos.
- exper (\(x_2\)): indica los años de experiencia laboral de cada persona en los datos.
Las seleccionaremos utilizando la función select() de dplyr, a modo de trabajar con un set de datos más acotado
wage1 = select(wage1, wage, educ, exper) #Seleccionamos sólo las variables por analizarRecordemos la distribución de estas variables:
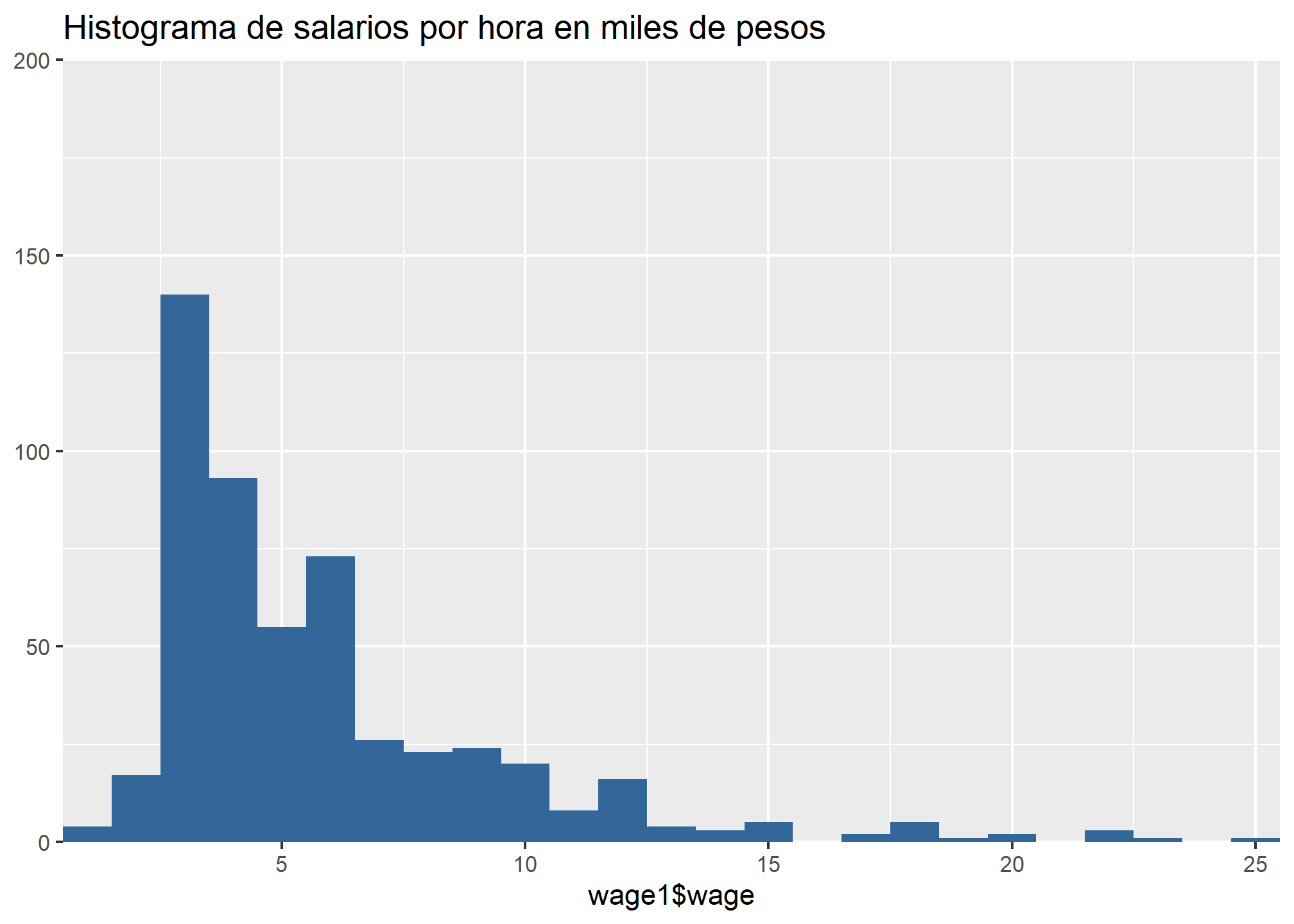
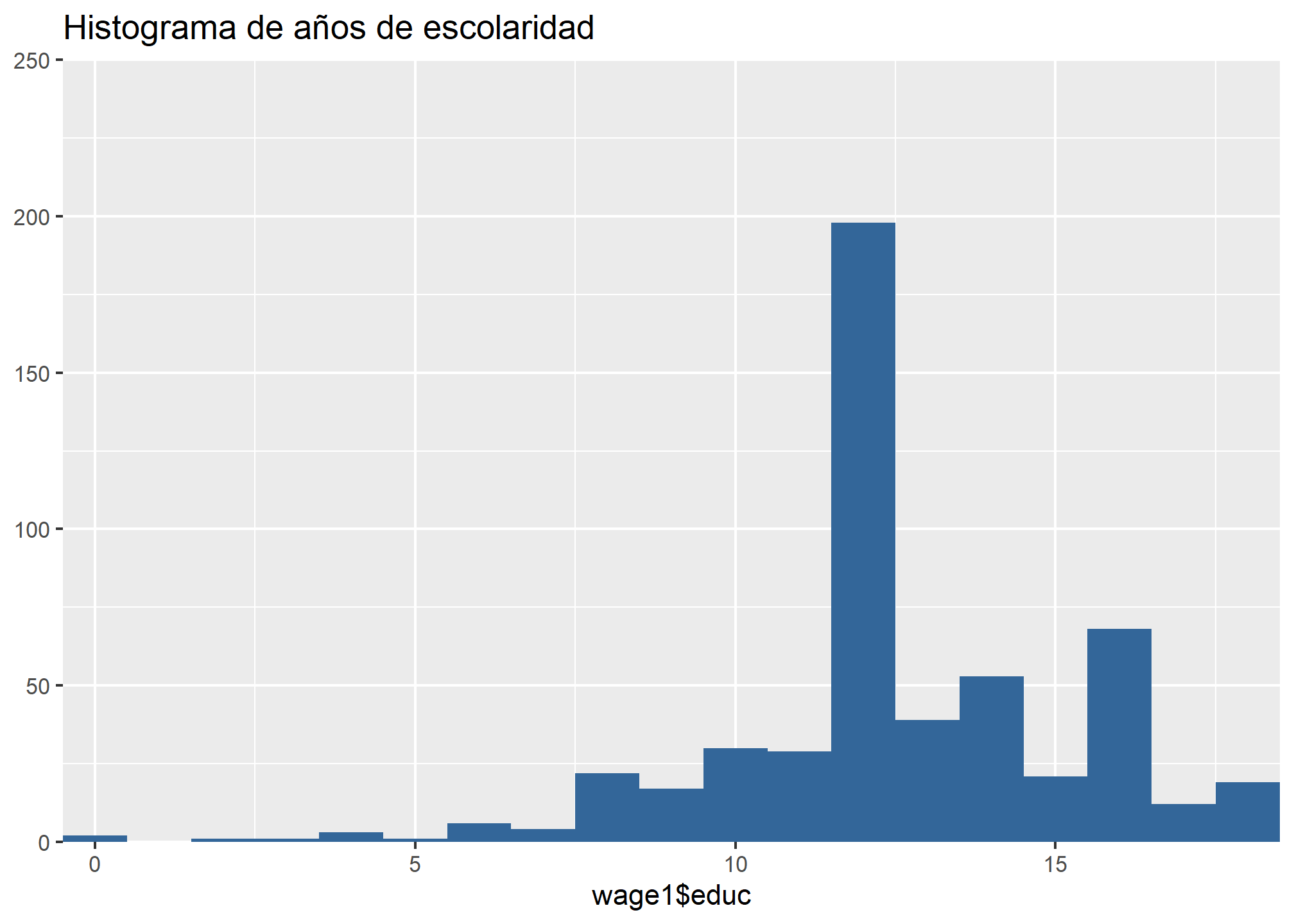
## Warning: Removed 1 rows containing missing values (geom_bar).
En este caso, la variable por explicar sigue siendo wage (\(y\)), a partir de la cual estimaremos un modelo de regresión lineal múltiple sobre educ (\(x_1\)) y exper (\(x_2\)). Un modelo de regresión lineal múltiple se puede expresar a partir de la siguiente ecuación:
\[ \begin{equation} \hat{y} = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} \end{equation} \] Donde
\(\beta_0\): Corresponde al intercepto de regresión.
\(\beta_1\): Corresponde a la pendiente estimada para la función de regresión lineal de los salarios por hora (\(y\)) sobre los años de escolaridad (\(x_1\)). Así, por cada unidad que aumente \(x_1\) (en este caso, por cada año de escolaridad extra), el valor estimado \(\hat{y}\) para los salarios por hora aumentará o disminuirá en \(\beta_1\).
\(\beta_2\): Corresponde a la pendiente estimada para la función de regresión lineal de los salarios por hora (\(y\)) sobre los años de experiencia laboral (\(x_2\)). Así, por cada unidad que aumente \(x_1\) (en este caso, por cada año de experiencia laboral), el valor estimado \(\hat{y}\) para los salarios por hora aumentará o disminuirá en \(\beta_2\).
En este caso, se podría plantear la hipótesis de que tanto educ como exper debiesen tener un efecto positivo sobre wage. Es decir, que
Quienes tengan más años de escolaridad debiesen tender, en promedio, valores predichos más altos que quienes tengan menos años de escolaridad. Así, se espera que \(\beta_1>0\); y
Quienes tengan más años de experiencia laboral debiesen tender, en promedio, valores predichos más altos que quienes tengan menos años de experiencia laboral. Así, se espera que \(\beta_2>0\).
Como sabemos, existe una correlación de 0.41 entre salarios por hora y años de escolaridad:
## `geom_smooth()` using formula 'y ~ x'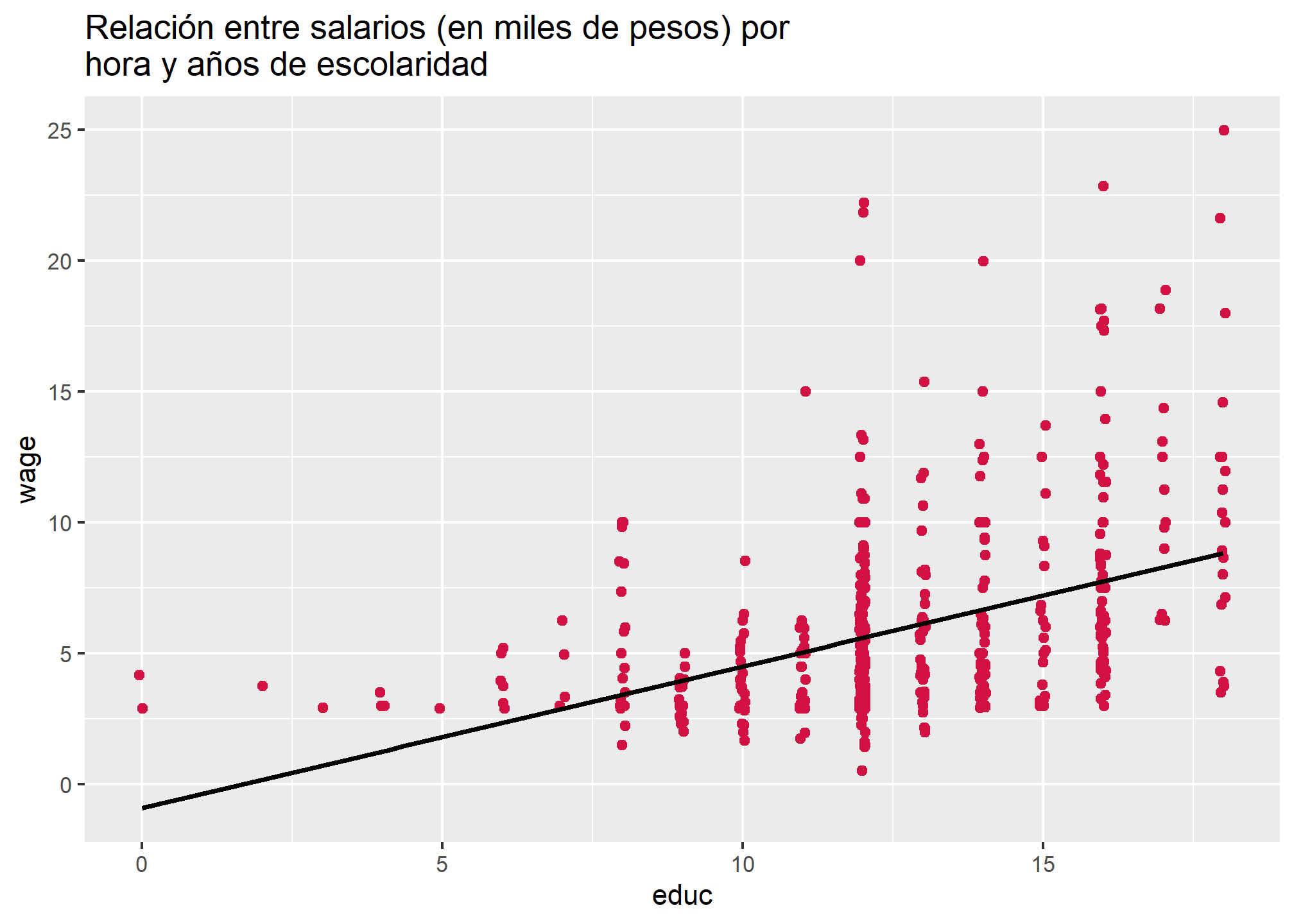
Por otra parte, esperamos que exista una asociación positiva entre salarios por hora y años de experiencia laboral
sjPlot::plot_scatter(wage1,
x = exper,
y = wage,
title = "Relación entre salarios (en miles de pesos) por hora y años de experiencia laboral",
fit.line = "lm")## `geom_smooth()` using formula 'y ~ x'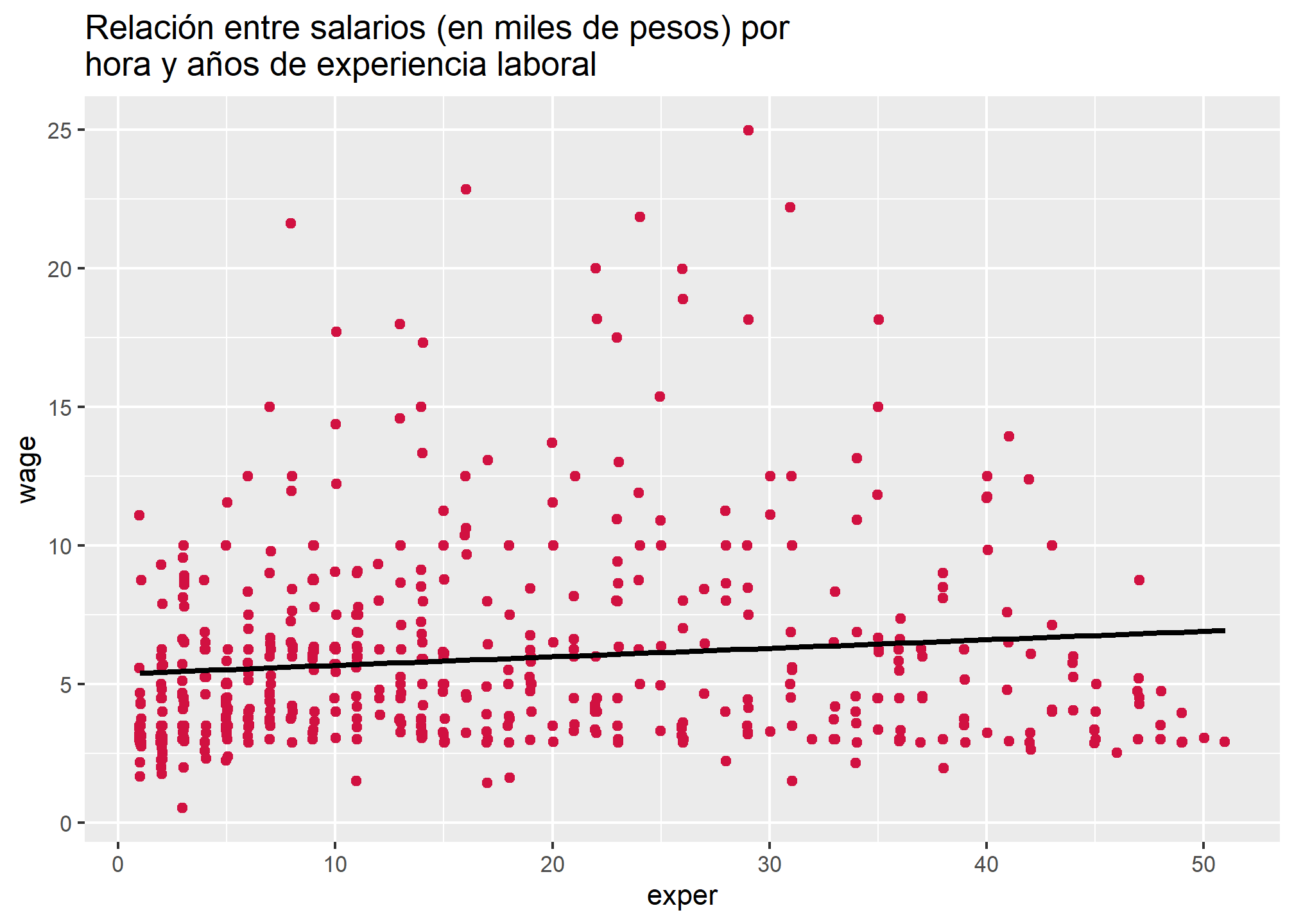
Como podemos ver, la pendiente de la recta de regresión presentada no tiene una pendiente tan acentuada, lo cual sería indicativo de una baja relación entre ambas variables. Sin embargo, puede surgir la duda respecto de qué tan relacionadas están nuestras dos variables explicativas. Explorémoslo
sjPlot::plot_scatter(wage1,
x = educ,
y = exper,
title = "Relación entre años de escolaridad y años de experiencia laboral",
fit.line = "lm")## `geom_smooth()` using formula 'y ~ x'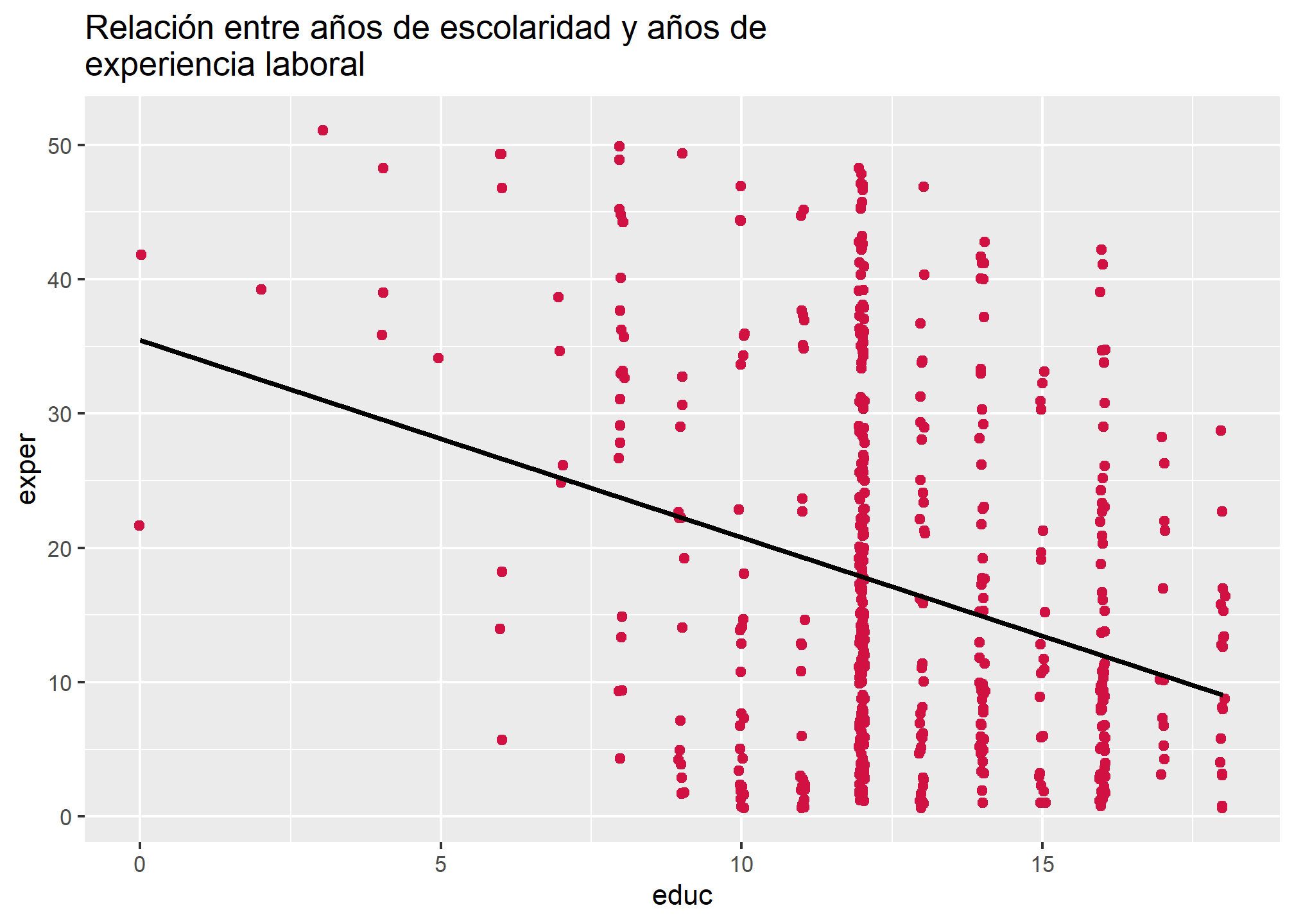
La siguiente tabla presenta los coeficientes de correlación de Pearson para todas las variables por analizar:
| wage | educ | exper | |
|---|---|---|---|
| wage | |||
| educ | 0.406*** | ||
| exper | 0.113** | -0.300*** | |
| Computed correlation used pearson-method with listwise-deletion. | |||
Como podemos ver, la asociación entre los años de experiencia laboral y los años de escolaridad es negativa y más fuerte que la correlación entre los primeros y el salario por hora. ¿Cómo puede esto afectar a la estimación de nuestro modelo? ¿qué efecto puede tener sobre la magnitud y el sentido de los coeficientes estimados? ¿cómo saber si vale la pena incorporar nuevas variables en el análisis? A continuación abordaremos todas estas inquietudes, retomando los conceptos que hemos estado revisando en las clases anteriores.
2. Estimando modelos de regresión lineal simple y múltiple con lm()
En términos de código, la estimación de modelos de regresión lineal simple no distan mucho de la estimación de modelos de regresión lineal múltiple. Estimemos el modelo para salarios por hora sobre años de escolaridad
\[ \begin{equation} \hat{wage} = \beta_0 + \beta_1educ_{i} \end{equation} \]
m1 = lm(wage ~ educ, data = wage1)Luego, el modelo para salarios por hora sobre años de experiencia laboral
\[ \begin{equation} \hat{wage} = \beta_0 + \beta_2exper_{i} \end{equation} \]
m2 = lm(wage ~ exper, data = wage1)Por último, el modelo para salarios por hora sobre años de escolaridad y años de experiencia laboral
\[ \begin{equation} \hat{wage} = \beta_0 + \beta_1educ_{i} + \beta_2exper_{i} \end{equation} \]
m3 = lm(wage ~ educ + exper, data = wage1)Como podemos ver, la única diferencia entre la estimación de un modelo de regresión lineal simple y uno múltiple con lm() es la incorporación de todas las variables explicativas, una tras otra, separadas por + (signo más).
Comparemos los tres modelos:
##
## ===============================================
## Modelo 1 Modelo 2 Modelo 3
## -----------------------------------------------
## (Intercept) -0.90 5.37 *** -3.39 ***
## (0.68) (0.26) (0.77)
## educ 0.54 *** 0.64 ***
## (0.05) (0.05)
## exper 0.03 ** 0.07 ***
## (0.01) (0.01)
## -----------------------------------------------
## R^2 0.16 0.01 0.23
## Adj. R^2 0.16 0.01 0.22
## Num. obs. 526 526 526
## ===============================================
## *** p < 0.001; ** p < 0.01; * p < 0.05Considerando las ecuaciones formuladas genéricamente más arriba, los modelos estimados se puede expresar así:
- Modelo 1 \[ \begin{equation} \hat{wage} = -.9 + .54educ_{i} \end{equation} \]
- Modelo 2
\[ \begin{equation} \hat{wage} = 5.37 + 0.03exper_{i} \end{equation} \]
- Modelo 3
\[ \begin{equation} \hat{wage} = -3.39 + .64educ_{i} + .07exper_{i} \end{equation} \]
Hay varias diferencias entre los tres modelos que podemos advertir:
El valor del intercepto de regresión es distinto entre los tres modelos.
Los valores de los coeficientes de regresión estimados para ambas variables son diferentes al incorporar ambas variables en conjunto.
La bondad de ajuste de los tres modelos expresada a través del estadístico \(R^2\) también difiere en los tres modelos, siendo mayor en el modelo 3 (\(R^2\) = .22).
Mientras que en los modelos 1 y 2 los estadísticos \(R^2\) y \(R^2\) Ajustado (Adj. \(R^2\)) son equivalentes, en el modelo 3 el valor de \(R^2\) (.23) y \(R^2\) Ajustado (.22) difieren en .01.
De ello podemos deducir que:
- Los años de escolaridad permiten explicar mejor que los años de experiencia laboral los salarios por hora promedio. Esto, porque
- El \(R^2\) del modelo 1 (.16) es mayor que el del modelo 2 (.01).
- La magnitud del coeficiente de regresión de años de escolaridad es mayor que la del coeficiente estimado para años de experiencia laboral.
- El efecto estimado de los años de escolaridad y años de experiencia laboral sobre los salarios por hora es positivo, tal como se planteó en la hipótesis al inicio del práctico.
- El modelo 3 permite explicar mejor la variabilidad de \(y\) que los modelos 2 y 1.
- El valor estimado para el estadístico \(R^2\) ajustado tiende a ser penalizado cuando se incorpora más de una variable explicativa; es decir, en modelos de regresión lineal múltiple, \(R^2 > Adj.R^2\). Por eso, en modelos múltiples es preferible evaluar la bondad de ajuste en base al estadístico ajustado, en la medida que es un criterio más estricto para definir qué tan bien las variables explicativas en su conjunto permiten explicar la variabilidad de \(y\).
¿Por qué sucede todo esto al incorporar una nueva variable explicativa? Para comprenderlo, recurriremos al concepto de parcialización.
3. La parcialización
Como pudimos ver anteriormente, educ está correlacionado negativa y moderadamente (R = -.3) con exper. Esto tiene como consecuencia que una parte del efecto de educ sobre wage es compartida por exper, y viceversa, lo cual genera cambios tanto en la estimación de los coeficientes de regresión como en la bondad de ajuste. Recordemos que lo que esperamos hacer con un modelo de estas características es aislar el efecto de \(x_1,x_2,...,x_n\) sobre \(y\). Es decir: poder analizar el efecto de \(x_1\) sobre \(y\), manteniendo constante el efecto del resto de variables involucradas en la variabilidad de \(y\). Considerando nuestro modelo 3 \(\hat{wage} = -3.39 + .64educ_{i} + .07exper_{i}\), ello se leería de la siguiente manera:
Por cada año de escolaridad adicional se espera que, en promedio, el salario por hora predicho aumente en .64 mil pesos, sin importar los años de experiencia que tenga la persona. Así, una persona con 20 años de experiencia, pero con 17 años de escolaridad debiese percibir un salario por hora promedio de 8.89 mil pesos; mientras se espera que, en promedio, alguien con los mismos años de experiencia laboral y 12 años de escolaridad obtenga un salario por hora de 5.69 mil pesos, lo cual expresa una diferencia media de 3.2 mil pesos.
Por cada año de experiencia laboral adicional se espera que, en promedio, el salario por hora predicho aumente en .07 mil pesos, sin importar los años de experiencia que tenga la persona. Así, una persona con 12 años de escolaridad, pero con 20 años de experiencia laboral debiese percibir un salario por hora promedio de 5.69 mil pesos; mientras se espera que, en promedio, alguien con los mismos años de escolaridad y 10 años de experiencia laboral obtenga un salario por hora de 4.99 mil pesos, lo cual expresa una diferencia media de 0.7 mil pesos.
Para poder realizar un análisis “manteniendo constante el efecto del resto de factores”, empleamos el procedimiento de parcialización, que consiste en remover la covarianza común que existe entre los predictores. A ello se le denomina efecto parcial, en la medida que estima regresión considerando solamente el efecto de \(x_n\) sobre \(y\) que no es compartido con los otros predictores. ¿Cómo saber cuál es la magnitud del efecto común a ambas variables y extraerlo? Para ello podemos modelar una regresión simple en que los predictores son las variables del modelo. En este caso, estimar un modelo que mida el efecto de educ sobre exper. Ello nos permitirá calcular, a su vez, los residuos del modelo entre las variables explicativas, que representa la parte de \(x_1\) que no es explicada por \(x_2\). A su vez, el coeficiente de regresión \(\beta_1\) representa todo lo compartido entre educ y exper. Estimemos el modelo:
mod_p = lm(educ ~ exper, wage1)
summary(mod_p)##
## Call:
## lm(formula = educ ~ exper, data = wage1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12.258 -1.358 -0.236 1.721 6.170
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 13.602708 0.185024 73.519 < 0.0000000000000002 ***
## exper -0.061113 0.008504 -7.187 0.0000000000023 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.644 on 524 degrees of freedom
## Multiple R-squared: 0.08973, Adjusted R-squared: 0.08799
## F-statistic: 51.65 on 1 and 524 DF, p-value: 0.000000000002295Así
\[ \begin{equation} \hat{educ} = 13.60 + 0.06exper_{i} \end{equation} \]
Estimemos los residuos para cada observación; es decir, la diferencia entre el valor predicho y el observado que, en este caso, representa la varianza no explicada de los años de experiencia laboral sobre los años de escolaridad.
pred = fitted.values(mod_p)
res = residuals(mod_p)
wage1 = cbind(wage1, pred, res)Ahora hagamos una regresión lineal de wage sobre los residuos estimados para el modelo de educ sobre exper
mod_res = lm(wage ~ res, wage1)
screenreg(list(m3, mod_res), custom.model.names = c("Modelo 3", "Modelo 4"))##
## ===================================
## Modelo 3 Modelo 4
## -----------------------------------
## (Intercept) -3.39 *** 5.90 ***
## (0.77) (0.14)
## educ 0.64 ***
## (0.05)
## exper 0.07 ***
## (0.01)
## res 0.64 ***
## (0.05)
## -----------------------------------
## R^2 0.23 0.21
## Adj. R^2 0.22 0.21
## Num. obs. 526 526
## ===================================
## *** p < 0.001; ** p < 0.01; * p < 0.05Podemos ver que el coeficiente estimado para educ en el modelo 3 es igual que aquel estimada para el modelo 4. Es decir, el coeficiente parcializado para los años de escolaridad estimado en el modelo 3 representa el efecto de la parte de educ que no es explicada por exper sobre wage. Como pueden haber intuido, la parcialización es un procedimiento que lm() realiza automáticamente a la hora de estimar los modelos, pese a lo cual es fundamental comprenderlo adecuadamente para poder entender qué significa analizar el efecto de \(x_n\) sobre \(y\) ceteris paribus.
En síntesis: la parcialización nos permite estimar y analizar el efecto parcial de \(x_n\) sobre \(y\), controlando el efecto de otras variables sobre \(y\).
Resumen
En este práctico aprendimos las diferencias existentes entre modelos de regresión lineal simple y múltiple, poniendo especial atención al concepto de parcialización.