Regresión lineal simple con diseño muestral y bondad de ajuste
0. Objetivo del práctico
El presente práctico tiene tres objetivos:
Analizar la bondad de ajuste de los modelos de regresión lineal simple estimados a través del estadístico \(R^2\).
Aprender a estimar una regresión lineal simple incorporando el diseño muestral en las estimaciones en R, a través de la función
svyglm().Comprender la importancia y las implicancias de realizar las estimaciones de modelos de regresión lineal, considerando u omitiendo el diseño muestral en el análisis.
Materiales de la sesión
Tal como en la sesión anterior, en este práctico se utilizarán los datos sobre salarios utilizados en el capítulo 2 del libro Introducción a la econometría de J.W. Wooldridge (2015).
Asimismo, la realización de este práctico requiere la carga de diversos paquetes que nos permitirán explorar los datos y presentar los modelos estimados.
if (!require("pacman")) install.packages("pacman") # Instalamos pacman en caso de necesitarlo
pacman::p_load(wooldridge, #Para descargar los datos
dplyr, #Para procesar datos
sjmisc, #Para explorar los datos
sjPlot, #Para explorar los datos
MCMCpack, #Para crear un ponderador ficticio
srvyr, #Para crear un objeto encuesta
survey, #Para realizar estimaciones incorporando el diseño muestral
texreg) #Para presentar el modelo de regresión estimado
data("wage1") #Cargamos los datos
wage1 = select(wage1, wage, educ) #Seleccionamos sólo las variables por analizar1. Recordemos: Estimando un modelo de regresión lineal simple con lm()
Como recordarán del práctico anterior, lo que buscamos es estimar un modelo de regresión lineal simple de salarios por hora (wage) sobre años de escolaridad (educ). La siguiente ecuación expresará, entonces, el efecto promedio de los años de escolaridad sobre el salario por hora, ceteris paribus
\[ \begin{equation} \hat{wage} = \beta_0 + \beta_1educ_{i} \end{equation} \]
Utilizando la función lm() del paquete base de R podemos estimar ese modelo de regresión lineal utilizando nuestros datos.
mod = lm(wage ~ educ, data = wage1)Luego de haber creado el objeto que contiene el modelo de regresión lineal simple estimado, debemos proceder a presentarlo para poder analizar los resultados. Para ello utilizaremos la función summary() de base.
summary(mod)##
## Call:
## lm(formula = wage ~ educ, data = wage1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.3396 -2.1501 -0.9674 1.1921 16.6085
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.90485 0.68497 -1.321 0.187
## educ 0.54136 0.05325 10.167 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.378 on 524 degrees of freedom
## Multiple R-squared: 0.1648, Adjusted R-squared: 0.1632
## F-statistic: 103.4 on 1 and 524 DF, p-value: < 0.00000000000000022La tabla nos informa que los años de escolaridad tienen un efcto positivo (\(\beta_1 = 0.54\)) sobre el salario por hora. Es decir, se espera que personas con más años de escolaridad tiendan a presentar, en promedio, salarios por hora más altos. Concretamente, por cada año de escolaridad adicional se espera que una persona tenga, en promedio, un salario promedio .54 mil pesos mayor.
Ajuste y residuos
Como podemos recordar, lo que se espera es que exista una relación lineal entre \(x\) e \(y\). La recta de regresión presentada en la siguiente figura representa los valores predichos para \(y\) por cada valor de \(x\). No obstante, no siempre los modelos que estimamos permiten ajustarse de manera perfecta a la variabilidad de los datos, lo que implica que existirá una diferencia entre los valores predichos para \(y\), respecto de los valores observados en la muestra. A esta diferencia entre \(\hat{y}\) e \(y\) se denomina residuo.
sjPlot::plot_scatter(wage1,
x = educ,
y = wage,
title = "Relación entre salarios (en miles de pesos) por hora y años de escolaridad",
fit.line = "lm")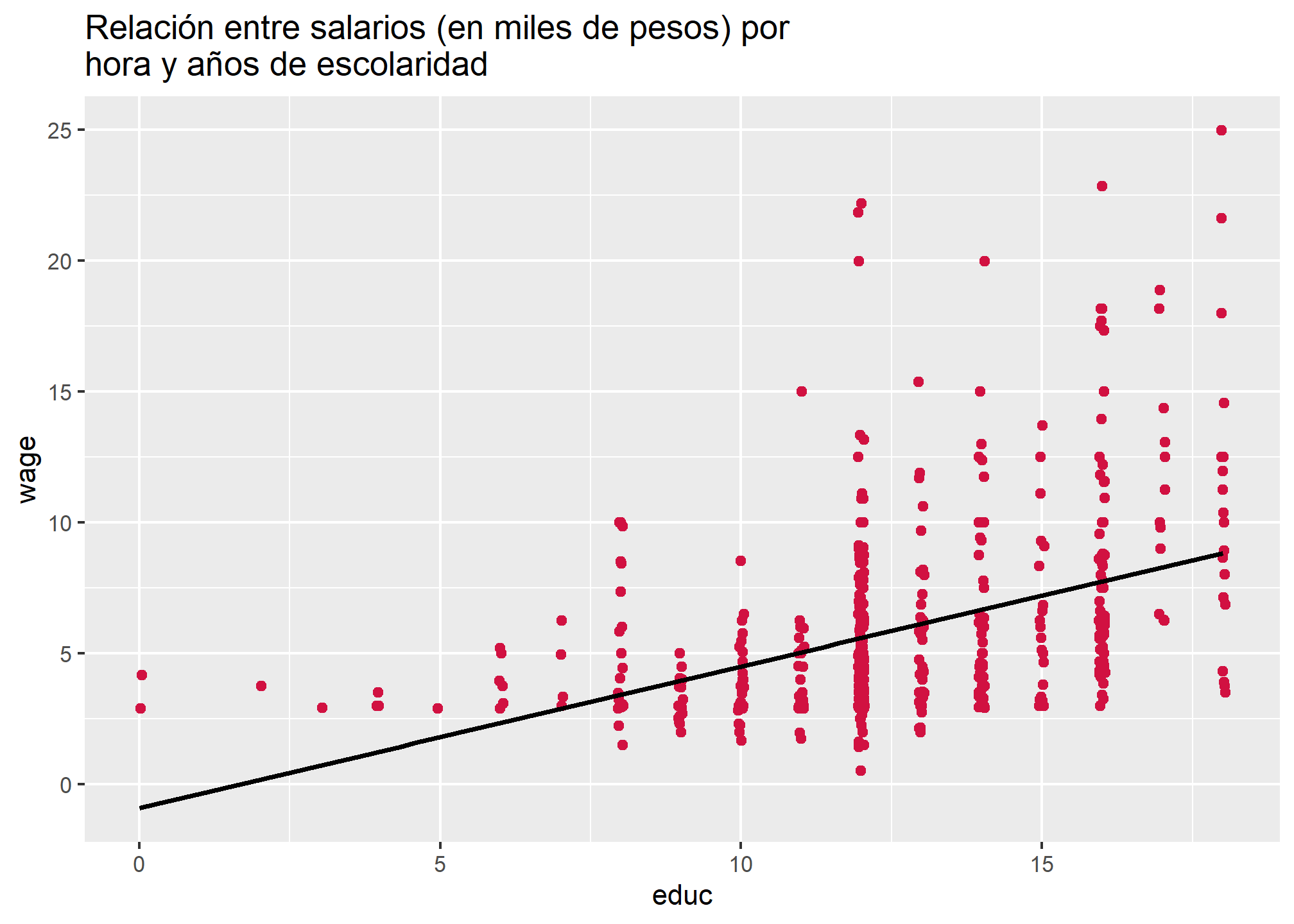
Aquellas observaciones que estén por sobre la recta serán residuos positivos o subestimaciones, pues en estos casos \(\hat{y}>y\), de modo que \(\hat{y}-y > 0\). Por el contrario, las observaciones bajo la recta constituyen residuos negativos o sobrestimaciones. Del mismo modo, los valores que se encuentran sobre la recta de la regresión fueron predichos de forma precisa por el modelo, por lo cual sus residuos tenderán a acercarse a cero.
En ese sentido, su objetivo como analistas de datos será hallar una recta que minimice lo más que se pueda el valor de los residuos, en tanto ello es indicativo de un modelo que permite explicar adecuadamente la variabilidad en \(y\) en razón de la variabilidad en \(x\). Como se señaló al final del práctico anterior, la minimización de la suma de los residuos al cuadrado o \(SS_{residual}\) permite optimizar la estimación de la recta de regresión: a esto se denomina método de Mínimos Cuadrados Ordinarios (MCO) (u OLS en inglés). La suma de los residuos se realiza al cuadrado para evitar que residuos positivos y negativos se anulen entre sí.
Sin embargo, dado que un mismo modelo de regresión puede representar distintas distribuciones de datos con distintos residuos, es necesario estimar estadísticos que reflejen la bondad de ajuste del modelo estimado. Así, podemos encontrar información que nos permita afirmar qué tan bien el modelo representa la distribución de los datos, o qué tan buena es la predicción estimada. Si bien para ello se podría simplemente calcular la cantidad de residuos generados por el modelo, ello desembocaría en un valor de difícil interpretación en términos de ajuste. Para ello se recurre a un estadístico llamado \(R^2\), que permite representar la bondad de ajuste del modelo de forma sencilla.
Este estadística varía entre 0 y 1, y da cuenta del porcentaje de la varianza de \(y\) que podemos explicar con \(x\). Un modelo que genera menos residuos, en consecuencia, también presenta un mayor valor en el estadístico \(R^2\). Un modelo donde todos los valores observados se ajustan perfectamente a la recta de regresión estimada presenta un \(R^2 = 1\).
2. Calculando \(R^2\)
Este estadístico se puede representar de la siguiente forma
\[ \begin{equation} R^2 = \frac{SS_{reg}}{SS_{tot}} \end{equation} \] , donde
- \(SS_{reg}\): corresponde a la suma de cuadrados de la regresión, y expresa la diferencia entre el valor predicho \(\hat{y}\) y el promedio de la variable explicada \(\bar{y}\). Esta valor se interpreta como la parte de \(y\) que es posible conocer si se conoce \(x\), o ¿qué tan útil resulta \(x\) para saber sobre la variabilidad de \(y\), más allá de \(\bar{y}\)? Para ello, sustraemos al valor predicho para cada caso el promedio de \(y\) y elevamos ese valor al cuadrado, para después sumar todos esos valores:
\[ SS_{reg} = \sum_{i=1}^{n}(\hat{y} - \bar{y})^2 \]
- \(SS_{tot}\): corresponde a la suma total de cudrados, es decir, la suma de las diferencias entre los valores observados de \(y\) y su promedio \(\bar{y}\), lo cual representa la varianza total de \(y\):
\[ SS_{tot} = \sum_{i=1}^{n}(y - \bar{y})^2 \]
Considerando la ecuación de la recta de regresión de salario por hora sobre años de escolaridad
\[ \begin{equation} \hat{y} = -.9 + .54 x_{i} \end{equation} \] Estimamos
predy: los valores predichos para \(y\) para cada una de las observaciones en la muestra,difpredprom: el cuadrado de la diferencia entre los valores predichos para \(y\) y el promedio de \(y\),difobsprom: el cuadrado de la diferencia entre los valores observados para \(y\) y el promedio de \(y\),
wage1$predy = -.9+(.54*wage1$educ)
wage1$difpredprom = (wage1$predy-mean(wage1$wage))^2
wage1$difobsprom = (wage1$wage-mean(wage1$wage))^2Utilizamos sum() para estimar \(SS_{reg}\) y \(SS_{tot}\)
sum(wage1$difobsprom)## [1] 7160.414sum(wage1$difpredprom)## [1] 1173.894Luego, reemplazamos y obtenemos
\[ \begin{equation} R^2 = \frac{SS_{reg}}{SS_{tot}} = \frac{1173.894}{7160.414} = 0.164 \end{equation} \]
Entonces, es posible señalar que el porcentaje de la varianza de los salarios por hora wage que es posible relacionar a los años de escolaridad educ corresponde al \(16.4\)%. Asimismo, un \(83.6\)% de la varianza de los salarios porn hora no está relacionada a los años de escolaridad.
Por supuesto, no es necesario realizar todo este cálculo manualmente para conocer la bondad de ajuste de nuestro(s) modelos. Funciones como texreg() (utilizada el práctico pasado) o summary presentan este estadístico en su output:
summary(mod)##
## Call:
## lm(formula = wage ~ educ, data = wage1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.3396 -2.1501 -0.9674 1.1921 16.6085
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.90485 0.68497 -1.321 0.187
## educ 0.54136 0.05325 10.167 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.378 on 524 degrees of freedom
## Multiple R-squared: 0.1648, Adjusted R-squared: 0.1632
## F-statistic: 103.4 on 1 and 524 DF, p-value: < 0.00000000000000022En este caso, el estadístico se presenta en la penúltima fila del output, luego del texto Multiple R-squared:. Podemos ver que el valor es bastante similar a la estimación a mano realizada. Como señalamos, lo esperado es obtener un \(R^2\) lo más elevado posible. Sin embargo, esto no es lo único que importa a la hora de estimar un modelo de regresión lineal: es fundamental que nuestro modelo esté fundamentado teórica y empíricamente, además de que este y los datos cumplan con una serie de supuestos que permiten asegurar que la estimación realizada es válida en términos estadísticos. Uno de estos supuestos es, por supuesto, que la muestra extraída sea probabilística y representativa de la población, a modo de poder realizar inferencias estadísticamente fundadas respecto de la relación entre \(x\) e \(y\) a nivel poblacional.
Para poder incorporar el efecto del diseño muestral en la población, independiente de si este es simple o complejo, debemos acudir a funciones distintas a lm(). Así, utilizaremos los paquetes srvyr y survey para elaborar un objeto encuesta y estimar modelos de regresión
3. Estimando un modelo de regresión lineal simple considerando un diseño muestral simple
Como hemos visto anteriormente, el modelo de regresión lineal tiene como estadístico base la media de \(x\) e \(y\). En este caso, \(\bar{x} = 12.56\) y \(\bar{y} = 5.89\). De incorporar el diseño muestral en la estimación de la media de ambas variables ¿se presentarán diferencias? Para saberlo, primero debemos crear un objeto encuesta que nos permita incorporar el diseño muestral de los datos en la estimación. En este caso, asumiremos que se trabaja con datos producidos a partir de un muestreo aleatorio simple. Además, crearemos un ponderador ficticio pond que nos permita realizar este ejercicio adecuadamente. Utilizaremos as_survey_design() de srvyr para crear nuestro objeto encuesta
#Creamos el ponderador ficiticio
npond <- 526
pond <- MCMCpack::rdirichlet(1, runif(npond)) |>
as.vector()
sum(npond)## [1] 526all(dplyr::between(pond, 0, 1))## [1] TRUEwage1 = cbind(wage1, pond)
enc = wage1 %>%
as_survey_design(weights = pond) #Especificamos la variable del ponderadorLuego, utilizamos survey_mean() de survey para estimar la media de ambas variables considerando el diseño muestral de los datos
enc %>%
summarise(x=survey_mean(educ))## # A tibble: 1 × 2
## x x_se
## <dbl> <dbl>
## 1 12.6 0.202enc %>%
summarise(y=survey_mean(wage))## # A tibble: 1 × 2
## y y_se
## <dbl> <dbl>
## 1 6.01 0.314Podemos ver que, a nivel poblacional, los valores estimados eran 12.56 y 5.89 para \(x\) e \(y\), respectivamente. Sin embargo, al considerar el diseño muestral en la estimación de estos valores, la media calculada cambia a 12.63 e 6.22, respectivamente. La incorporación de ponderadores en la estimación permite ajustar esta última a la probabilidad de cada uno de los sujetos de ser elegidos en la muestra. De ese modo, podemos estimar los valores de \(\bar{x}\) e \(\bar{y}\) a nivel poblacional, considerando el error muestral en la estimación.
Lo mismo sucede con los valores estimados para \(\beta_0\) y \(\beta_1\): incorporar el diseño muestral en la estimación del modelo de regresión permite ajustar los valores obtenidos para el intercepto y los coeficientes de regresión, acercándolos al parámetro poblacional. Para llevar esto a cabo en R recurrimos a svyglm() de survey, que permite estimar distintos modelos de regresión (que no revisaremos en este curso), entre los cuales se encuentra el modelo de regresión lineal, considerando el diseño muestral de los datos. El código se construye de manera muy similar a como lo hacíamos con lm(). Las únicas salvedades son
- En lugar de especificar los datos, debemos especificar el objeto encuesta generado, y
- Dado que esta función permite estimar diversos tipos de modelos lineales generalizados, debemos especificar en el argumento
family =que el modelo que deseamos estimar es lineal.
mod_enc = svyglm(wage ~ educ, #Especificamos la fórmula
design = enc, #Especificamos el objeto encuesta
family = gaussian(link = "identity")) #Especificamos el modelo linealComparemos los modelos con y sin la consideración el diseño muestral en su estimación:
##
## ====================================
## Sin Con
## ------------------------------------
## (Intercept) -0.90 -0.88
## (0.68) (1.36)
## educ 0.54 *** 0.55 ***
## (0.05) (0.12)
## ------------------------------------
## R^2 0.16
## Adj. R^2 0.16
## Num. obs. 526 526
## Deviance 6626.61
## Dispersion 12.62
## ====================================
## *** p < 0.001; ** p < 0.01; * p < 0.05Es posible apreciar que los valores estimados difieren ligeramente para ambos modelos. Ello involucra tanto el intercepto y el coeficiente de regresión, como a sus errores estándar y medidas de ajuste. Esto significa que la inclusión del diseño muestral en la estimación del modelo tiene consecuencias para la inferencia estadística que puede hacerse a partir de él. De este modo se puede justificar la incorporación del diseño muestral en la estimación de modelos de regresión siempre que sea posible, pues mejora su validez al mejorar su precisión, acercando el intercepto y los coeficientes generados a los valores que alcanzan en la población.
Resumen
En este práctico aprendimos las diferencias de estimar modelos de regresión lineal simple con y sin la incorporación del diseño muestral complejo en sus estimaciones. Además, a través del estadístico \(R^2\), aprendimos a analizar la bondad de ajuste de los modelos estimados.