1. Familiarizándose con los datos

Como se señalo anteriormente, se trabajará con datos sobre salarios. Para cargarlos, utilizamos la función data("wage1")

data("wage1")

Nos daremos cuenta de que en nuestro ambiente ha aparecido un dataframe con 526 observaciones y 24 columnas. Particularmente, en este caso trabajaremos con dos variables:

wage: indica el salario por hora en miles de pesos de cada persona en los datos.
educ: indica el número de años de escolaridad de cada persona en los datos.

Las seleccionaremos utilizando la función select() de dplyr, a modo de trabajar con un set de datos más acotado

wage1 = select(wage1, wage, educ)

Como se ha revisado en las clases, el análisis de regresión busca cuantificar la relación entre dos variables \(x\) (independiente, predictora, explicativa, entre otros) e \(y\) (dependiente, predicha, explicada, entre otros). En particular, se busca

Explicar \(y\) en términos de \(x\), o bien
Analizar cómo varía \(y\) cuando varía \(x\).

En este práctico se busca estimar un modelo de regresión lineal de wage (\(y\), variable explicada) sobre educ (\(x\), variable explicativa). Antes de adentrarse directamente en la comprensión y estimación de los modelos de regresión lineal simple, es relevante explorar uni y bivariadamente los datos por analizar. Para ello, nos valdremos de las funciones descr() del paquete sjmisc, que permite describir variables cuantitativas; plot_frq() y plot_scatter de sjPlot para análisis uni y bivariados;y cor() del paquete base de R.

Descriptivos univariados con `sjmisc::descr()` y `sjPlot::plot_frq()`

En general, variables de niveles de medición intervalar o de razón (también denominadas genéricamente como variables cuantitativas) permiten emplear una serie de propiedades de los números que se traducen en la posibilidad de realizar con ellos operaciones aritméticas como sumar, restar, multiplicar y dividir. Así, es posible estimar para ellas no sólo medidas de posición, sino también otras medidas de tendencia central de gran importancia como, en particular, la media, así como medidas de dispersión tales como la varianza. Ambos estadísticos son fundamentales en la estimación de modelos de regresión lineal.

En particular, los descriptivos para la variable wage se obtienen

sjmisc::descr(wage1$wage)

## 
## ## Basic descriptive statistics
## 
##  var    type label   n NA.prc mean   sd   se   md trimmed              range
##   dd numeric    dd 526      0  5.9 3.69 0.16 4.65    5.24 24.45 (0.53-24.98)
##   iqr skew
##  3.55 2.01

Siguiendo lo presentado es posible distinguir que, en la muestra, los salarios por hora oscilan entre los .53 y los 24.98 mil pesos chilenos. El promedio es de 5.9 mil pesos por hora, mientras que la desviación estándar corresponde a 3.69 mil pesos por hora. Además, la mediana (4.65 mil pesos por hora) es inferior a la media, lo cual indicaría una asimetría positiva en los datos. Considerando una jornada laboral de 44 horas semanales, lo anterior nos indica que, en promedio, los trabajadores de la muestra obtienen un salario mensual promedio de 1038400 pesos.

Un histograma también puede ser útil para identificar la distribución de la variable:

sjPlot::plot_frq(wage1$wage,
                 title = "Histograma de salarios por hora en miles de pesos",
                 type = "histogram")

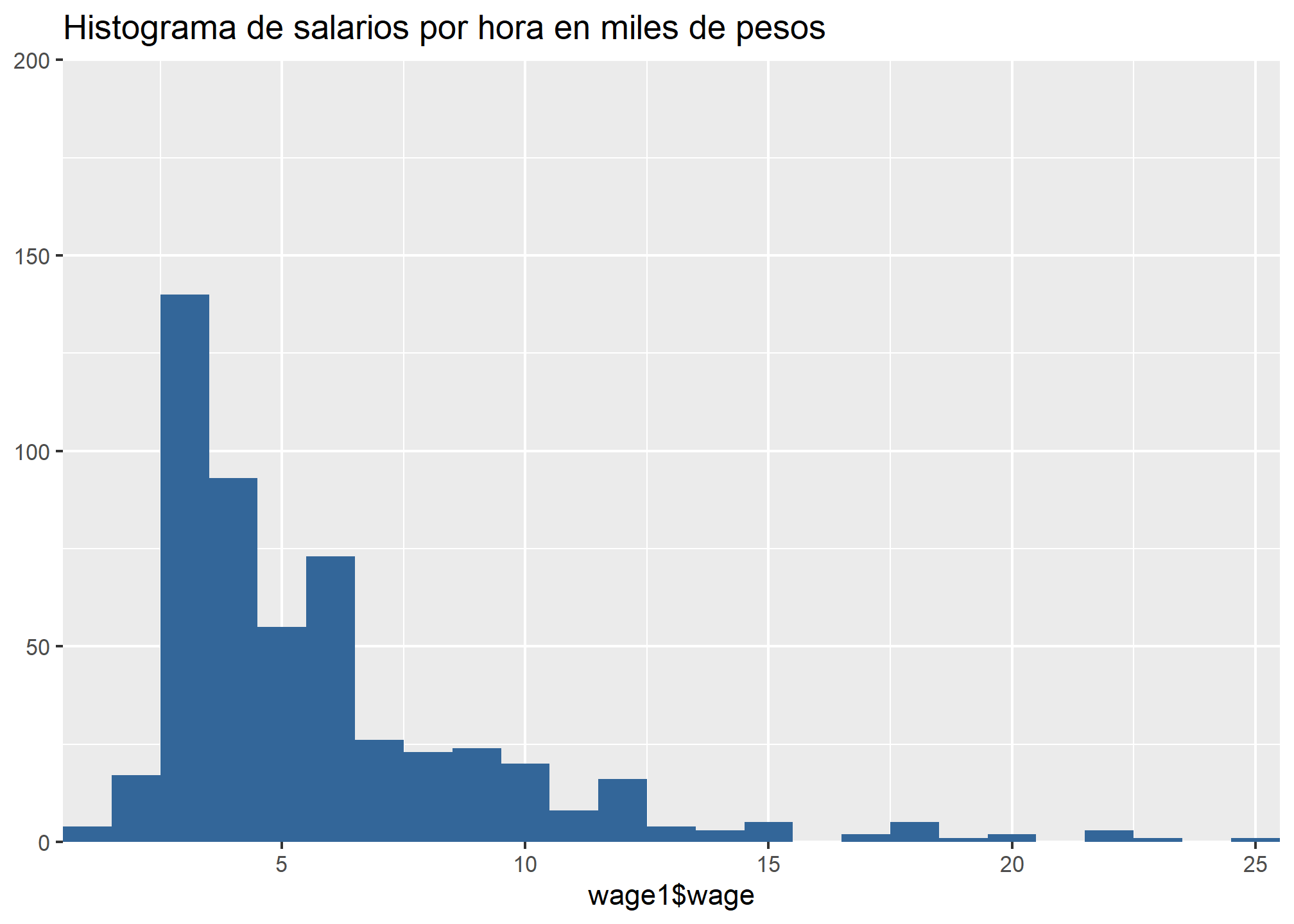
En este caso, es posible apreciar que la distribución de la variable presente una asimetría positiva, lo cual indica que la mayoría de los datos se concentran en la zona inferior de la distribución (es decir, hay una mayor proporción de salarios por hora bajos en relación con salarios por hora muy altos).

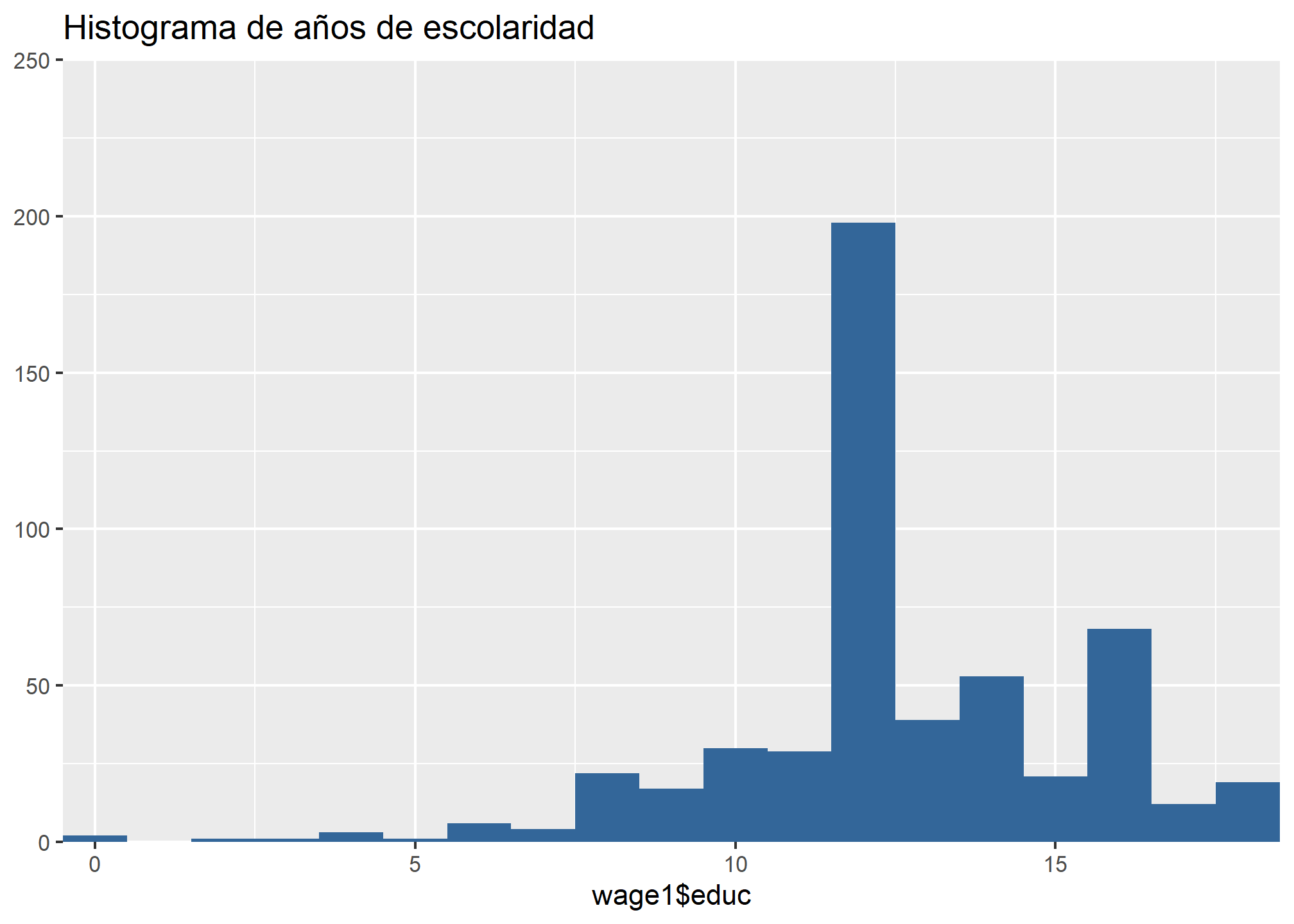
En el caso de los años de escolaridad, la media corresponde a 12.56 años, con una mediana de 4.65 años y una desviación estándar de 3.69. Ello indica que al menos un 50% de las personas en la muestra completaron la enseñanza media.

descr(wage1$educ)

## 
## ## Basic descriptive statistics
## 
##  var    type label   n NA.prc  mean   sd   se md trimmed     range iqr  skew
##   dd integer    dd 526      0 12.56 2.77 0.12 12   12.69 18 (0-18)   2 -0.62

En lo que respecta a la distribución de la variable educ, es posible constatar que la mayoría de los casos se encuentran en torno a la media, que corresponde a 12.56 años de escolaridad, lo cual corresponde a un nivel educacional medio.

sjPlot::plot_frq(wage1$educ,
                 title = "Histograma de años de escolaridad",
                 type = "histogram")

Análisis bivariado con `base::cor()` y `sjPlot::plot_scatter()`

Entre otros elementos, algo fundamental que tenemos que considerar a la hora de plantear la estimación de un modelo que busque analizar el efecto de \(x\) sobre \(y\) es que estas deben estar relacionadas entre sí, al menos de forma moderada. Para estimar la correlación entre dos variables utilizamos base::cor()

cor(wage1$wage, wage1$educ)

## [1] 0.4059033

En este caso la correlación es de 0.41, lo cual corresponde a una relación moderada-fuerte en ciencias sociales. Es posible graficar esta relación con sjPlot::plot_scatter() para analizar con mayor detalle la asociación entre salarios por hora y años de escolaridad

sjPlot::plot_scatter(wage1, 
                     x = educ, 
                     y = wage,
                     title = "Relación entre salarios (en miles de pesos) por hora y años de escolaridad",
                     fit.line = "lm")

## `geom_smooth()` using formula 'y ~ x'

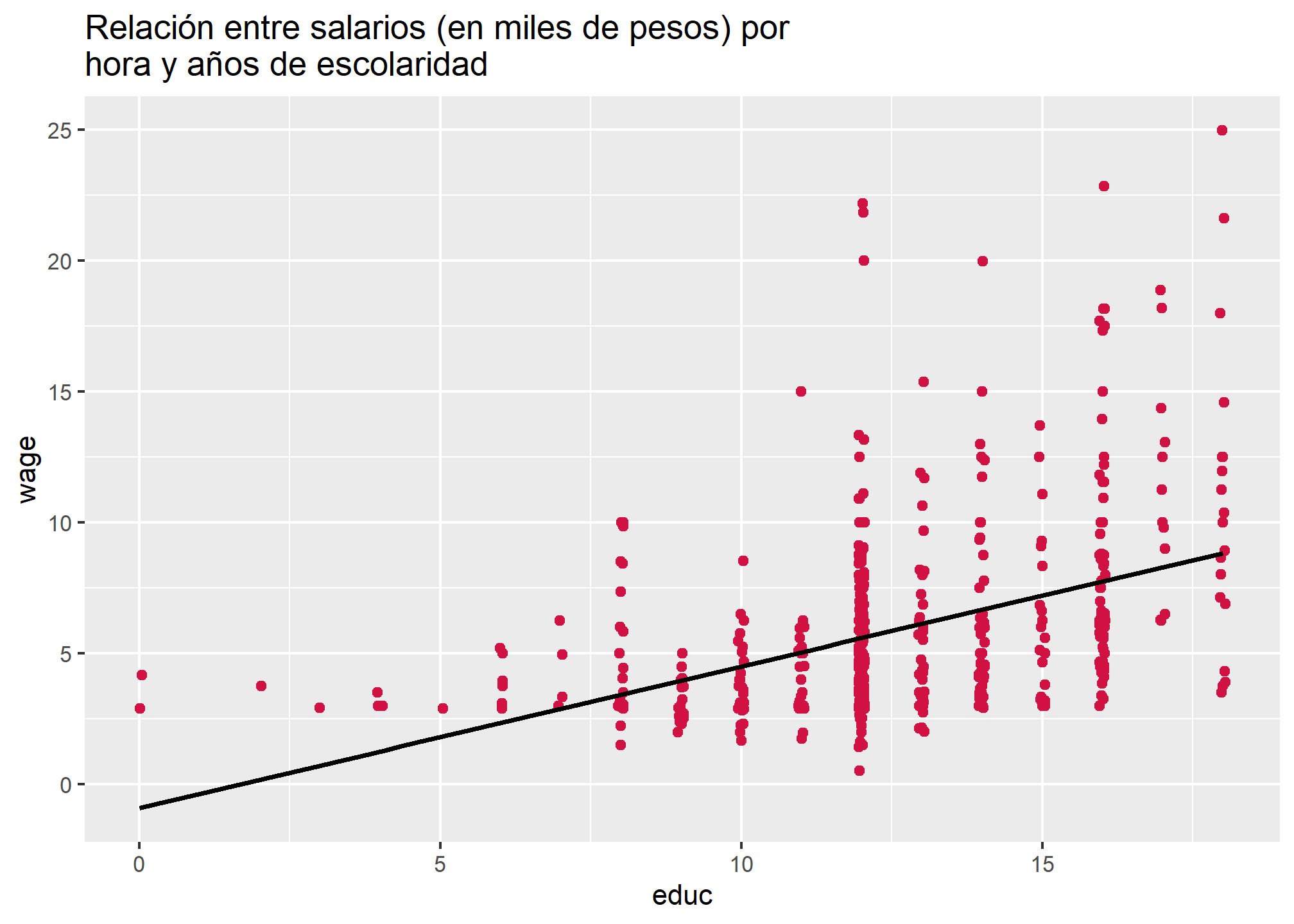
Si bien no hay claridad de que la relación entre ambas variables sea lineal dada la recta de regresión presentada (lo cual es el supuesto fundamental del análisis de regresión lineal), si se puede identificar una relación positiva entre salarios por hora y años de escolaridad. Ello apoya la hipótesis planteada al inicio del práctico: una mayor escolaridad estará asociada, en promedio, a salarios por hora más elevados.

2. Estimando un modelo de regresión lineal simple con `lm()`

En general, la estimación de modelos de regresión lineal simple en R es sencilla en términos de código. Antes de ello, sin embargo, consideremos la formalización del modelo de regresión lineal por estimar

\[ \begin{equation} \hat{wage} = \beta_0 + \beta_1educ_{i} + u_{i} \end{equation} \] Es decir: el salario por hora predicho corresponde a la suma del intercepto de regresión \(\beta_0\), más el valor estimado para el coeficiente de regresión \(\beta_1\) estimado para la variable educ por el valor observado en esa variable para cada sujeto, más el error \(u_{i}\) asociado a cada observación. En términos generales:

\(\beta_0\): Corresponde al valor estimado para \(\hat{y}\) para alguien con cero años de escolaridad.
\(\beta_1\): Corresponde a la pendiente estimada para la función de regresión lineal de \(\hat{y}\) sobre \(x\). Así, por cada unidad que aumente \(x\) (en este caso, por cada año de escolaridad extra), el valor estimado \(\hat{y}\) para los salarios por hora aumentará o disminuirá en \(\beta_1\).
\(u_{i}\): Corresponde al error en la estimación, generado por la no incorporación en el modelo de variables que estén relacionadas con wage. En este caso, incluir variables como el área de actividad económica, la ocupación, la capacidad de liderazgo o resolución de problemas, entre otros, puede disminuir el error causado por la no observación de efectos estadísticamente significativos de estas variables sobre los salarios por hora.

Sin embargo, para simplificar el análisis, en el práctico sólo nos enfocaremos en \(\beta_0\) y \(\beta_1\). Para estimar un modelo de regresión simple, debe utilizarse el siguiente código

mod = lm(wage ~ educ, data = wage1)

En términos sencillos, el anterior código indica a R que

Cree un nuevo objeto llamado mod (recordemos que = indica asignación);
Este nuevo objeto será un modelo de regresión lineal estimado con lm(),
En el cual la variable explicada \(y\) corresponde a wage (lo que antecede a ~),
Mientras que la variable explicativa \(x\) corresponde a educ (lo que sucede a ~),
Utilizando los datos del objeto wage1.
Es decir: lm(\(y\) ~ \(x_1\), datos).

Luego de ejecutar ese código, se generará en el ambiente un objeto llamado mod, que corresponde a una lista con 12 elementos. No nos adentraremos en ello en esta clase, pues el foco está en la estimación y comprensión estadística de los modelos de regresión lineal simple.

3. Comprendiendo el output de `lm()`

Luego de haber creado el objeto que contiene el modelo de regresión lineal simple estimado, debemos proceder a presentarlo para poder analizar los resultados. Para ello utilizaremos la función screenreg() de texreg.

screenreg(mod)

## 
## =======================
##              Model 1   
## -----------------------
## (Intercept)   -0.90    
##               (0.68)   
## educ           0.54 ***
##               (0.05)   
## -----------------------
## R^2            0.16    
## Adj. R^2       0.16    
## Num. obs.    526       
## =======================
## *** p < 0.001; ** p < 0.01; * p < 0.05

En la tabla se presentan diversos estadísticos. Revisemos los resultados con mayor atención, fila por fila:

Model 1: Indica el modelo presentado. Esto es útil en casos donde presentamos más de un modelo.
(Intercept): Indica el valor estimado para el intercepto de regresión o \(\beta_0\). Ello indica que, cuando \(educ_i = 0\), el salario por hora predicho corresponde a -.9 mil pesos. El valor en paréntesis que le sigue corresponde al error estándar estimado para el intercepto.
educ: Corresponde al coeficiente de regresión estimado para la variable explicativa educ, o \(\beta_1\). De ese modo el modelo estima que, por cada año de escolaridad que se aumente, el salario por hora predicho aumentará en .54 mil pesos. El valor en paréntesis que le sigue corresponde al error estándar estimado para el coeficiente.
R^2 y Adj. R^2: Corresponden a las medidas de ajuste del modelo. Esto se revisará con detención en el práctico 5.
Num. obs: Número de observaciones con las cuales se estimó el modelo. En este caso, se utilizó la totalidad de la muestra, que cuenta con 526 casos. Es fundamental considerar que la estimación de modelos de regresión lineal sólo utiliza observaciones que cuenten con casos válidos en \(x\) y en \(y\), por lo cual el trabajo de procesamiento de datos es fundamental para lograr un buen análisis.
*** p < 0.001; ** p < 0.01; * p < 0.05: Indican el p-valor estimado para cada coeficiente. Esto se abordará con profundidad en el práctico 8.

Así, siguiendo la formalización planteada anteriormente y los resultados obtenidos, es posible plantear que

\[ \begin{equation} \hat{wage} = -.9 + .54 educ_{i} \end{equation} \]

4. Interpretando un modelo de regresión lineal simple

Ahora sólo nos falta interpretar el modelo estimado. Para ello hay que tomar en cuenta los valores estimados para \(\beta_0\) y \(\beta_1\)

\(\beta_0\): Como se señaló anteriormente, el intercepto corresponde al valor predicho \(\hat{y}\) cuando \(x_1 = 0\). En este caso, indica el salario por hora predicho en promedio para personas con 0 años de escolaridad.
\(\beta_1\): en este caso, el valor positivo del coeficiente (\(\beta_1 > 0\)) indica que existe un efecto positivo de los años de escolaridad sobre el salario por hora predicho: mientras más años de escolaridad se tengan, más alto debiese ser el salario por hora percibido. En términos concretos: se espera que, en promedio, una persona con 11 años de escolaridad perciba un salario por hora .54 mil pesos más alto que alguien con 10 años de escolaridad. Es posible estimar los valores predichos para corroborarlo:

\[ \begin{equation} \hat{wage_1} = -.9 + .54 educ_{i} = -.9 + .54*10 = 4.5 \end{equation} \] \[ \begin{equation} \hat{wage_2} = -.9 + .54 educ_{i} = -.9 + .54*11 = 5.04 \end{equation} \] Luego, \(5.04-4.5 = .54 = \beta_1\).

De lo anterior se sigue que

Se espera que \(\beta_1 \neq 0\) pues, de lo contrario, no existiría un efecto estadísticamente significativo de \(x_1\) sobre \(y\).
Asimismo, mientras mayor sea \(|\beta_1|\), mayor será la magnitud del efecto de \(x_1\) sobre \(y\) y viceversa.
Si \(\beta_1 > 0\), el efecto de \(x_1\) sobre \(y\) es positivo.
Si \(\beta_1 < 0\), el efecto de \(x_1\) sobre \(y\) es negativo.

5. ¿Cómo se estima \(\beta_{1}\)?

Como es posible constatar, la estimación de modelos de regresión lineal simple en R es bastante sencilla en términos de código: lo más relevante es indicar claramente cuál es la variable \(x\), y cuál es la variable \(y\). Sin embargo, es importante comprender conceptual y matemáticamente cómo se estima \(\beta_1\).

Como se señaló al inicio del práctico, el método de estimación de Mínimos Cuadrados Ordinarios (MCO) (u OLS en inglés). Ello indica que la estimación busca optimizar una recta que se ajuste a los datos disminuyendo al máximo la suma de los residuos al cuadrado. Los residuos se elevan al cuadrado para sumarlos, lo cual se denomina Suma de residuos al cuadrado o \(SS_{residual}\). Esto para evitar que residuos positivos y negativos se anulen entre sí.

Ahora ¿qué son los residuos? Estos corresponden a la diferencia entre el valor predicho y el valor observado. Si, por ejemplo, el salario por horas predicho corresponde a 4 mil pesos, y el valor observado corresponde a 3.7 mil pesos por hora, entonces el residuo de la estimación para esta observación equivale a -.3 mil pesos.

Considérese la ecuación

\[ \begin{equation} \hat{y} = \beta_0 + \beta_1x_{i} \end{equation} \] , donde

\(\beta_0 = \hat{y} - \beta_1\);
\(\beta_1 = \frac{Cov(XY)}{VarX}\), donde
- \(Cov(XY) = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{n-1}\), y
- \(VarX = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})}{n-1}\)

Luego, es posible simplificar de la siguiente manera

\[ \begin{equation} \beta_1 = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})} = \frac{\sum_{i=1}^{n}(y_i - \bar{y})}{\sum_{i=1}^{n}(x_i - \bar{x})} \end{equation} \]

A continuación, crearemos variables que reflejen la diferencia entre los valores observados \(x_i\) e \(y_i\) y el promedio \(\bar{x}\) y \(\bar{y}\), respectivamente:

wage1$difx = wage1$educ-mean(wage1$educ)
wage1$dify = wage1$wage-mean(wage1$wage)

Con ello procedemos a calcular la diferencia de productos cruzados \((x_i - \bar{x})(y_i - \bar{y})\), y la diferencia de cada valor observado de \(x\) con su promedio al cuadrado \((x_i - \bar{x})^2\)

wage1$difcru = wage1$difx*wage1$dify
wage1$difx2 = wage1$difx^2
head(wage1)

##   wage educ       difx       dify     difcru      difx2
## 1 3.10   11 -1.5627376 -2.7961028  4.3695751  2.4421489
## 2 3.24   12 -0.5627376 -2.6561027  1.4946890  0.3166737
## 3 3.00   11 -1.5627376 -2.8961027  4.5258487  2.4421489
## 4 6.00    8 -4.5627376  0.1038973 -0.4740562 20.8185748
## 5 5.30   12 -0.5627376 -0.5961025  0.3354493  0.3166737
## 6 8.75   16  3.4372624  2.8538973  9.8095938 11.8147725

Así, es posible obtener la suma de productos cruzados \((x_i - \bar{x})(y_i - \bar{y})\), y la suma de cuadrados de X \((x_i - \bar{x})^2\)

sum(wage1$difcru)

## [1] 2179.204

sum(wage1$difx2)

## [1] 4025.43

Reemplazamos los valores en la fórmula anterior:

\[ \begin{equation} \beta_1 = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})} = \frac{2179.204}{4025.43} = 0.54 \end{equation} \]

Y estimamos el intercepto reemplazando por valores ficticios

\[ \begin{equation} \beta_0 = \hat{y} - \beta_1x_i = 6.12-(.54*13) = 6.12*7.02 = -.9 \end{equation} \] Así, la ecuación estimada manualmente es idéntica a la estimada a través de lm()

\[ \begin{equation} \hat{y} = -.9 + .54 x_{i} \end{equation} \]

Desafío: estimando \(\beta_{1}\)

¡Ahora es su turno! Utilizando la tabla presentada a continuación, deben estimar manualmente el valor de \(\beta_1\), siguiendo los pasos detallados recientemente

print(head(wage1[,1:2], 10))

##     wage educ
## 1   3.10   11
## 2   3.24   12
## 3   3.00   11
## 4   6.00    8
## 5   5.30   12
## 6   8.75   16
## 7  11.25   18
## 8   5.00   12
## 9   3.60   12
## 10 18.18   17

La correcta realización del desafío significará una bonificación individual de .5 décimas en la nota obtenida en la prueba del curso ¡mucha suerte!

0. Objetivo del práctico

Materiales de la sesión

1. Familiarizándose con los datos

Descriptivos univariados con `sjmisc::descr()` y `sjPlot::plot_frq()`

Análisis bivariado con `base::cor()` y `sjPlot::plot_scatter()`

2. Estimando un modelo de regresión lineal simple con `lm()`

3. Comprendiendo el output de `lm()`

4. Interpretando un modelo de regresión lineal simple

5. ¿Cómo se estima \(\beta_{1}\)?

Desafío: estimando \(\beta_{1}\)

Resumen

0. Objetivo del práctico

Materiales de la sesión

1. Familiarizándose con los datos

Descriptivos univariados con sjmisc::descr() y sjPlot::plot_frq()

Análisis bivariado con base::cor() y sjPlot::plot_scatter()

2. Estimando un modelo de regresión lineal simple con lm()

3. Comprendiendo el output de lm()

4. Interpretando un modelo de regresión lineal simple

5. ¿Cómo se estima \(\beta_{1}\)?

Desafío: estimando \(\beta_{1}\)

Resumen

Descriptivos univariados con `sjmisc::descr()` y `sjPlot::plot_frq()`

Análisis bivariado con `base::cor()` y `sjPlot::plot_scatter()`

2. Estimando un modelo de regresión lineal simple con `lm()`

3. Comprendiendo el output de `lm()`